Retro Review: Casio FC-1000 Financial Consultant
Birthday post!
Quick Facts:
Model: FC-1000 Financial Consultant
Company: Casio
Years: 1988-early 1990s
Type: Finance and Graphic
Batteries: 3 x CR-2025
Memory: 2,470 programming steps
Contrast wheel
Like the Casio fx-7500G, the FC-1000 is a foldable calculator which is very small and light.
Features
The main modes of the FC-1000 are come in two categories: system modes and calculation modes.
System Modes
Run Mode (Mode 1): This mode is for calculations and running programs.
Write Mode (Mode 2): This mode is for writing programs, in one of 10 slots, Prog 0 to Prog 9.
Program Clear Mode (Mode 3): Erase programs in this mode. Clear all programs by pressing [ SHIFT ] [ DEL ] ( Mcl ).
Calculation Modes
Financial Mode (Mode 4): This mode is for financial calculations including time value of money (simple/compound/monthly C.I.), amortization, D.C.F. (discounted cash flows including NPV, IRR, NFV), bonds, depreciation, and cost/sell/margin. The financial calculations are accessed by pressing the [ MENU ] key. One of the great things of the FC-1000 is that it has a big screen to list variables and menu choices.
Linear Regression Mode (Mode 5): This mode fits bivariate data to the equation y = a + bx.
SD Mode (Mode 6): Single variable statistics
Mathematical Functions
The FC-1000 has a set of mathematical functions tailored to financial calculations:
* powers and roots
* logarithms
* integer and fraction parts
* factorials of positive integers
* days between dates
How to figure out how to calculate days between dates:
month_before [ DATE ] day_before [ DATE ] year_before [ DATE ] [ - ]
month_after [ DATE ] day_after [ DATE ] year_after [ DATE ]
If a two digit year is entered, it is implied that the year is 19##. Thankfully four digits years are allowed, so this calculator can be used in the 21st century. (Trivia: I will be alive 16,436 days today using the 365 day mode).
The date separate is indicated by a forward slash.
Programming
The FC-1000 uses the Casio basic programming language. The following commands available are:
Comparisons and the jump command:
[ test ] ⇒ [ do if true ] : or ◢ [ skip to here if false ]
Goto and label commands (Lbl 0-9)
Count jumps Isz (increment and skip on zero) and Dsz (decrement and skip on zero)
We can also store values in financial variables that are accessed through the menu system.
As mentioned before, the space has a capacity of 2,470 steps over 10 program slots.
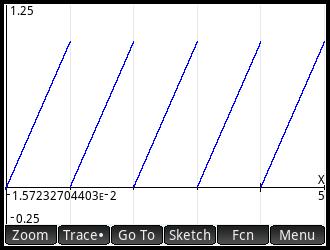
Graphing
The FC-1000 has graphing, but is limited to certain financial applications: bonds, amortization, and depreciation. Depending on what type of graph, pressing [ Trace ] will highlight the next period, and [ Shift ] [ Trace ] will rotate between different points of data.
For instance, in bonds, the [ Shift ] [ Trace ] combination rotates between price (PRC), coupon (CPN), and redemption value (RDV).
In amortization, the cycle is interest (INT), principal (PRN), and the nth payment (n).
In depreciation, the cycle is the year's depreciation (Depr) and year (n).
Closing Thoughts
I love the form factor of the FC-1000 and how compact the calculator is. However, the calculator is light weight and extra care is a must. I wish the graphing module allowed us to graph functions and added statistical graphs.
The FC-1000 can be difficult to collect, hence prices may be higher than a lot of vintage calculators.
Until next time,
Eddie
All original content copyright, © 2011-2022. Edward Shore. Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited. This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author.