Retro Review: Sears Electronic Slide Rule

Retro Review: Sears Electronic Slide Rule

Quick Facts

Model: Electric Slide Rule,  801.58771

Company: Sears

Production Years:  1974 - mid 1970s

Power:  Battery, originally AA chargeable NiCad*

Type:  Scientific

Operating System:  Chain

Memory Registers:  1

Display:  One line:  8 digits, 2 lights:  one for overflow (error), one for negative numbers

Same Key Set as:   Rockwell 61R

*  I purchased this calculator at the Pasadena City College Swap Meet on July 2, 2023.  The calculator is in great condition, along with a great leather case and instruction manual.   The calculator was re-configured to run on 4 regular AA batteries, to that I'm very grateful.

Keyboard and Scientific Functions 

Most of the functions available are shifted functions.  The equals key is in an usual place, on the 2nd row from the top, above the arithmetic keys.  Access the shifted functions (written in white) by pressing the black key [ f ]. 

Scientific Functions Available:

Logarithm:  ln, log, e^x, 10^x

Roots and Powers:  √x, x^y, 1/x

Trigonometry:  sin, cos, tan, arc (inverse)

Memory Functions:  m+, m-, m+x^2  (add the square of a display to memory) x←m (recall), x→m (store), x←→m (exchange with memory), x←→y (swap arguments, not shifted) 

DR:  Data Recovery function is activated the key sequence [ f ] [ f ] (not a typo, DR is the shifted function of [ f ]).  What this does is two-fold:

1.  Erase the last number entered.

2.  Activate the intended shifted function without having the need to press [ f ] again.

Example:  e^4

[ 4 ] [ 4 ]:   Display:  44

[ f ] [ f ]:   Erases the last 4,  Display:  4

[ 4 ]:  Calculates e^4, Display:  54.59814

CF:  Clear Function.   Cancels out the shifted function [ f ].

Example:  12 + 89

[ 1 ] [ 2 ] [ + ]

[ f ]:   next key pressed will be a shifted function

[ c ce ] (cf):  cancels out that shifted function

[ 8 ] [ 8 ] [ = ]:  Display: 100

There are two switches:  Power (On/Off) on the left, and Angle mode (Degrees/Radians) on the right.  

Negative Numbers

There was no room on the display for a negative sign (apparently), instead negative numbers are indicated by a bright red light on the upper right hand of the display, next to the clear Neg imprint on the screen.  

I would prefer the negative sign on the display, to the left of the number.  

Chain Mode

The Slide Rule operates in chain mode, which is the calculations happen exactly the way they are entered, with no respect to the order of operations.   Note that there are no parenthesis keys.

For example:

4 + 3 × 8 returns 56

3 × 8 + 4 returns 28

Powers

Assume that n is a positive integer.

a^n  can be accomplished by entering a, repeatedly pressing [ × ] n-1 times, finishing by pressing [ = ].

7^5:  7 [ × ] [ × ] [ × ] [ × ] [ = ].  Result:  16807

[ × ] four times. 

1/(a^n) can be accomplished by entering a, repeatedly pressing [ ÷ ] n+1 times, finish by pressing [ = ].

4^-3:  

4 [ ÷ ]:  Display:  4

[ ÷ ]:  Display:  1   (4^0 = 1)

[ ÷ ]:  Display:  0.25   (4^-1 = 1/4)

[ ÷ ]:  Display :  0.0625  (4^-2 = 1/16)

[ = ]:  Display:  0.015625  (4^-3 = 1/64)

The power function x^y operates on the formula e^(y × ln x).   This may lead to rounding errors.  

Example:

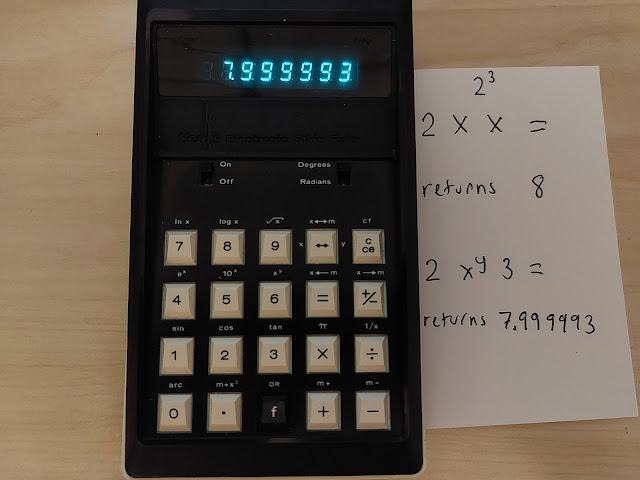
2^3 = 8.

2 [ × ] [ × ] [ = ]  returns 8.   The exact answer.

2 [ f ] [ 6 ] (x^y) 3 [ = ] returns 7.999993

Floating Point Rounding Errors

One drawback of the Electronic Slide rule is the rounding floating point errors.  

70 [ f ] [ ÷ ] (1/x)  returns 0.0142857

Press [ f ] [ ÷ ] (1/x) again returns 70.00007

0.5 [ f ] [ 0 ] (arc) [ 2 ] (cos) returns 59.99999 degrees (it should be 60 degrees)

The forensic test returns 10.4382 (9 sin cos tan arctan arccos arcsin).  

I think the calculator can handle numbers to what the display capacity allows.  There is no internal guard digits to help with accuracy.    

Final Thoughts

I like the feel of the calculator.   The screen has large green numbers which makes the display easy to read.   The keys are are pretty responsive, especially back in the day when it comes to lower-cost calculators in the 1970s (around $100).  

I am not the biggest fan of the negative number indicator, the Rockwell 61R has a negative sign.  Not a deal breaker, though.  The good thing is that red indicator light is bright.  

The Slide Rule is great for fans of Chain Mode (non-algebraic mode).   

If you buy one be sure that:  the charging cord and rechargeable batteries are included and in good working order or the calculator is modified to work on regular AA batteries.

I like how the manual goes in depth with the operations and its library of applications.  

Sources:

Download the manual from Katie Wasserman's Page:  

Sears Electronic Slide Rule:  

https://www.wass.net/manuals/Sears%20Slide%20Rule.pdf

Rockwell 61R:

https://www.wass.net/manuals/Rockwell%2061R.pdf

calculator.org's page on the  Sears Electronic Slide Rule (retrieved July 2, 2023):

https://www.calculator.org/calculators/Sears_Electronic_Slide_Rule.html

Eddie

All original content copyright, © 2011-2023.  Edward Shore.   Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited.  This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author. 

Σ(1 / (a^n)) from n=1 to m

 Σ(1 / (a^n)) from n=1 to m

This blog entry covers the sum of the series:

Σ[1 / (a^n), n=1 to m] with n and m positive integers

Specific Cases:  a = 2 and a = 3

When a = 2:

m = 1:   1/2

m = 2:   1/2 + 1/4  = (2 + 1)/4 = 3/4

m = 3:   1/2 + 1/4 + 1/8 = (4 + 2 + 1)/8 = 7/8

m = 4:   1/2 + 1/4 + 1/8 + 1/16 = (8 + 4 + 2 + 1)/16 = 15/16

Going from the pattern,

Σ[1 / (2^n), n=1 to m] = 1/(2^m) * Σ[(2^n), n=0 to m-1] = (2^m - 1) / 2^m 

When a = 3:

m = 1:  1/3

m = 2:  1/3 + 1/9  = (3 + 1)/9 = 4/9

m = 3:  1/3 + 1/9 + 1/27 = (9 + 3 + 1)/27 = 13/27

m = 4:  1/3 + 1/9 + 1/27 + 1/81 = (27 + 9 + 3 + 1)/81 = 40/81

Going from the pattern,

Σ[1 / (3^n), n=1 to m] = 1/(3^m) * Σ[(3^n), n=0 to m-1]

Finding the General Formula and Proof

Let's presume that, for any a:

Σ[1 / (a^n), n=1 to m-1] = 1/(a^(m-1) * Σ[(a^n), n=0 to m-2]

Let's add 1/(a^m) to the series:  

Σ[1 / (a^n), n=1 to m-1]  + 1/(a^m)

= (1 + a + a^2 + ... + a^(m-3) + a^(m-2)) / (a^(m-1)) + 1 / (a^m)

= (a * (1 + a + a^2 + ... + a^(m-3) + a^(m-2)) + 1) / (a^m)

= (a + a^2 + a^3 + ... + a^(m-2) + a^(m-1) + 1) / (a^m)

= 1/(a^(m)) * Σ[(a^n), n=0 to m-1]

The general formula is now: 

Σ[1 / (a^n), n=1 to m] = 1/(a^(m)) * Σ[(a^n), n=0 to m-1]

Until next time,

Eddie

All original content copyright, © 2011-2021.  Edward Shore.   Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited.  This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author. 

Retro Review: Novus 4510 - Mathematician

Retro Review: Novus 4510 - Mathematician

Happy Labor Day!   Hopefully you are safe, healthy, and sane.

Quick Facts:

Model: 4510, also known as Mathematician

Company: National Semiconductor

Years: 1975 - 1977

Memory Register:  1 independent memory, cleared when it is turned off

Battery:  1 9-volt battery, could be powered by a certain AC Volt plugs

Screen:  LCD, 8 digits

A RPN Calculator from the 1970s

The Mathematician is a Reverse Polish Notation (RPN) calculator.  On an RPN calculator, instead of an equals key, you have an ENTER key to separate numbers and execute an operation to complete the calculation.

Examples:

400 ÷ 25 = 16

Keystrokes: 

400 ENT 25 ÷

(21 × 5) + (11 × 13) = 248

Keystrokes:

21 ENT 5 × 11 ENT 13 × + 

√(3^2 + 2^3) ≈ 3.3166238

Keystrokes:

3 [ F ] (x^2) ENT 2 ENT y^x + √

Forensic Results:

3 × 1/3 returns .99999999

asin(acos(atan(tan(cos(sin(60°)))))) returns 59.25697°

Keyboard

The keyboard of Novus 4510 has gray and ivory keys.  The font is a light gray against a black background, with shifted functions are in yellow, which gives the fonts great contrast.  The keys are rubbery and soft, and thankfully, the 4510 I was purchased had working keys.  

The Basic Set of Functions

The 4510 has a basic set of scientific functions:  principal square root, square root, powers, reciprocal, logarithms and exponents, and trigonometric functions.  The angle mode will always be in degrees.   The deg and rad commands are not mode settings, they are conversions:  deg changes angles from radians to degrees, and rad changes angles from degrees to radians.

There is no scientific notation on the 4510.  You are limited to 8 digits.  Anything over beyond ±99,999,999 will cause an error.

Any errors will be displayed by .0.0.0.0.0.0.0.0.

There is only one memory register.  The storage arithmetic functions available are M+, M-, and M+x^2 (square the value on the x register and adds it to memory).

The Stack of Three Levels

The 4510 has three stack levels:  x, y, z.    How the stack reacts depends on which operation is executed.  For example:

The ENT (Enter) Key:

x, y, z ->  x, x, y

The Arithmetic Operators (+, -, ×, ÷):

x, y, z ->  result, y, 0

The contents of the z stack are zeroed, which unusual for RPN calculators.

The functions x^2, √, 1/x, rad, deg:

x, y, z -> result, y, z

The Trigonometric, Exponential, and Exponential Operators (sin, cos, tan, and their inverses, log, ln, e^x):

x, y, z -> result, y, 0

The contents of the z stack are zeroed, which unusual for RPN calculators.

That makes for a very particular set up due to the usual stack operations, for example:  

sin 30° sin 40° sin 60°

Key strokes: 

30 sin 40 sin 60 sin × × returns the very incorrect answer 0

However:

30 sin 40 sin × 60 × returns the correct approximation .27833519

There is a swap key but there is no roll down key.    

Verdict

I like operating the 4510.  However, my biggest gripes are the way the stack is used depending on the operation, and the lack of operations and statistics.  It's good for a basic RPN calculator.  

Sources

"National Semiconductor Novus Mathematics Handled Electronic Calculator"  National Museum of American History Behring Center.  Washington, D.C.  Accessed August 15, 2021.  https://americanhistory.si.edu/collections/search/object/nmah_1305810

"Novus 4510 (Mathematician)"  calculator.org:  the calculator home page.  Flow Simulation Ltd. 2021  Accessed August 14, 2021.  https://www.calculator.org/calculators/Novus_4510.html

Eddie

All original content copyright, © 2011-2021.  Edward Shore.   Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited.  This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author. 

HP Prime and TI-84 Plus CE: Tetration, Iterated Exponentiation

HP Prime and TI-84 Plus CE: Tetration, Iterated Exponentiation

Introduction

Tetration is iterated exponentiation.  A common notation of tetration is the use of two upward arrows, known as Knuth’s up-arrow notation.  In general:

x ↑ ↑ y = x ^ x ^ x ^ … ^ x   (y times)

Take the x to its own power y times. 

For example:

2 ↑ ↑ 2 = 2 ^ 2 ^ 2 = 2 ^ 4 = 16

3 ↑ ↑ 2 = 3 ^ 3 ^ 3 = 3 ^ 27 = 7625597484987

 4 ↑ ↑ 2 = 4 ^ 4 ^ 4 = 4 ^ 256 =

13407807929942597099574024998205846127479365820592393377723561443721764030073546976801874298166903427690031858186486050853753882811946569946433649006084096

≈ 1.34078078079299 * 10^154

First, thank goodness that the HP Prime can handle really long integers in CAS mode.  Second, you can quickly see how fast the results grow in tetration calculations. 

In order to allow for a larger set of calculations, the programs are provided, where we break down the mantissa and exponents of each result. 

HP Prime Program TETRATION

EXPORT TETRATION(X,Y)

BEGIN

// 2018-08-14 EWS

LOCAL I,M,E,S;

// X^^Y, Y is an integer

M:=MANT(X);

E:=XPON(X);

FOR I FROM 1 TO Y DO

S:=M*ALOG(E)*LOG(X);

M:=ALOG(FP(S));

E:=IP(S);

END;

RETURN {M,E};

END;

  

TI-84 Plus CE Program TETRATION

"EWS 2018-08-14"

Disp "TETRATION X^^Y","Y: INTEGER"

Prompt X,Y

10^(fPart(X))→M

iPart(log(X))→E

For(I,1,Y)

M*10^(E)*log(X)→S

10^(fPart(S))→M

iPart(S)→E

End

Disp M,"*10^",E

Source:

“Knuth’s Up-Arrow Notation” Wikipedia.  Last edited August 9, 2018.  Retrieved August 14, 2018.  https://en.wikipedia.org/wiki/Knuth%27s_up-arrow_notation

Eddie

All original content copyright, © 2011-2018.  Edward Shore.   Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited.  This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author.  Please contact the author if you have questions.