Fun with the FX-603P Emulator
Author for the Emulator:
Martin Krischik
Cost: $5.99 (there is an fx-602P scientific calculator
emulator for $4.99, similar programming language but only 10 programming spaces
instead of 20)
The app is emulates the 1990 Casio fx-603P calculator.
Decibels to Pressure
Program: (29 steps)
“DB?” HLT ÷ 20 = 10^x
* 2E-5 = “Pressure:” HLT
Examples:
DB = 30 dB; Result:
6.32455532 * 10^-4 N/m^2
DB = 120 dB; Result:
20 N/m^2
Turn Performance
Given a plane’s true air speed (TAS in knots), stall speed
(in knots), and required bank turn (in degrees), the following are calculated:
1. G force
2. Normal stall speed
for the plane during the turn (knots)
3. Turn diameter
(nautical miles)
4. Time it takes for
the turn to be complete (in minutes)
Formulas:
G = 1/(cos(bank))
Stall speed = normal stall speed * √G
Diameter = TAS^2 / (34208 * tan(bank))
Time = (0.0055 * TAS) / tan(bank)
Memory Registers:
Input:
M00 = TAS, M01 = Stall speed, M02 = Bank
Output:
M03 = G force, M04 = resulting stall speed, M05 = diameter,
M06 = time
Program: (110 steps)
DEG “TAS?” HLT Min00
“Norm. Stall?” HLT Min01
“Bank?” HLT Min02
MR02 cos 1/x Min03
“G:” HLT
MR03 √ * MR01 =
“Stall Speed:” HLT
MR00 x^2 ÷ ( MR02
tan * 34208 ) = Min05 “Diameter:” HLT
0.0055 * MR00 ÷ MR02
tan “Time:” HLT Min06
Notes:
DEG: [ MODE ] [ 4 ]
Example:
Inputs:
TAS: 123 knots
Norm. Stall: 60 knots
Bank: 44.8°
Results:
G: 1.409302674
Stall Speed: 71.22843498 knots
Diameter: 0.445363387
n.m.
Time: 0.681239424 minutes (about 40.87 seconds)
Source: “Turn
Performance” HP 65 Aviation Pac-1 Hewlett Packard. 1974
.
Sum of a Function
This program uses the subroutine (under P9 with the variable
MinF, or any register M04 or after) to calculate the summation:
Σ f(x) for x = a to b
The sum is stored in M03.
Note: when entering a new f(x), clear P9 (MODE, 3, P9, AC)
first before entering the new function.
It’s a lot cleaner.
Main Program: (34
bytes)
0 Min03
“a?” HLT Min01
“b?” HLT Min02
MR02 – MR01 + 1 =
Min00
Lbl0
MR01 GSBP9 M+03
1 M+01
DSZ Goto0
MR03 “Σ=”
Note:
Lbl0: [ LBL] [ 0 ]
GSBP9: [GSB] [ P9 ]
Goto0: [ GOTO ] [ 0 ]
The character Σ: (in
ALPHA) [SHIFT] [ 7 ]
Memory F: [ Min ], [
MR ], etc. [EXE] for F.
Examples:
Σ n^2 + 3*n – 6 for n = 1 to 8
Subroutine:
Min0F x^2 + 3 * MR0F
– 6 =
Result: 264
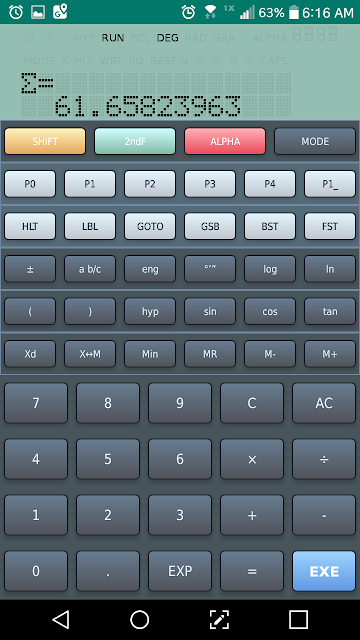
Σ (n^3 – 1)/(n^2 + 1) for n = 0 to 11
Subroutine:
( Min0F x^y 3 – 1 )
/div (MR0F x^2 + 1 ) =
Result: 61.6582396282
Combinations: where Repetition is allowed
The program calculates the number of combinations where
repeats are allowed.
nHr = (n + r – 1)! / (r! * (n -1)!)
Program: (39 steps)
“n?” HLT Min01
“r?” HLT Min02
( MR01 + MR02 – 1)
x!
÷ ( MR02 x! * ( MR01
– 1 ) x! )
= “nHr=”
Examples:
Input: n = 5, r = 3.
Result: 35
Input: n = 12, r = 6.
Result: 12376
Aviation: Rate of
Climb
This program calculates the rate-of-climb (ft/min) when
plane increases the elevation (in feet) given the distance to the mountain (in
nautical miles, n.m.) and the true air speed (TAS, in knots).
Formula:
ROC = ( TAS * ΔALT )
/ (60 * √(dist^2 + (ΔALT/6077.1155)^2) )
Program: (88 steps)
6077.1155 Min0F
“TAS (knots)?” HLT
Min01
“CHG ALT (ft)?” HLT
Min02
“DIST (n.m.)?” HLT
Min03
( MR01 * MR02 ) ÷
( 60 * ( MR03 x^2 +
(
MR02 ÷ MR0F ) x^2
) √ = “ROC:”
Example:
Input:
TAS = 87 knots
CHG ALT = 4800 ft
DIST = 13.3 n.m.
Result:
522.3878955 ft/min
Source: “Rate of
Climb and Descent” HP 65 Aviation Pac-1 Hewlett Packard. 1974
Eddie
All original
content copyright, © 2011-2018. Edward
Shore. Unauthorized use and/or
unauthorized distribution for commercial purposes without express and written
permission from the author is strictly prohibited. This blog entry may be distributed for
noncommercial purposes, provided that full credit is given to the author. Please contact the author if you have
questions.