App
Review: SciPro Math - Campusano (Apple
iOS)
Note: This is a review of the first version of the app. According to their Instagram page, Version 2 is going to be released in February 2018. I look forward to what SciPro Math has in store.
Title:
SciPro Math
Author: Robert
Antonio Campusano Acotsa of Unlimited Power
Platform:
iOS
Price: $4.99 (January 2018), $9.99 thereafter
Version:
unknown
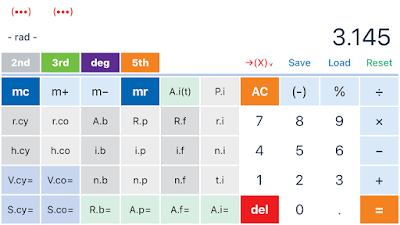 |
| Screen shots from SciPro Math |
Introduction
The SciPro Math calculator app by Unlimited
Power is a scientific calculator that features over 400 functions, including many
applications such as conversions, linear, quadratic, cubic, and quartic
equations, geometry formulas, linear systems, and finance. Depending on the
orientation of your device (iPhone or iPod Touch), the app either is a basic
calculator (portrait) or scientific calculator (landscape). This review will focus on the scientific
calculator.
Scientific
Calculators: Four Modifier Keys!
The calculator has four modifier keys: [ 2nd ], [
3rd ], [ rad ] which acts like the 4th key and displays [ deg ] when its turned on, and [ 5th ].
The [ rad ] key is also the angle toggle. When gray, the calculator is in degrees
mode. When the 4th key is turned on, the
calculator is in radians mode.
Unlike most scientific calculators when
modifiers are turned on for one keystroke, the modifiers on the SciPro Math,
stay on until the user turns the modifier off.
You can have more than one modifier turned on (even all four) at
once. This is important because the
keyboard changes depending on what modifier keys are turned on. The SciPro Math website will give the keyboard
layout, so I will just summarize the possible keyboards here:
Modifiers Turned On
|
Keyboard
|
None
|
Trig:
sin, cos, tan
Hyperbolic:
sinh, cosh, tanh
Other:
10^x, log, e^x, ln, x^3, x^2, square root, cube root, random numbers from
0 to 1, golden ratio constant (ϕ), reciprocal, π
Also sci, csi, and bta (bi-tangent). I don’t know what these functions are.
Storage variables: A, B, C
|
2nd
|
Trig: csc, sec, cot
Hyperbolic: csch, sech, coth
Other: logarithms of base 2, e^(-x), ln(1+x),
e^(x-1), gamma constant (γ), x^-2, power, root, absolute value, factorial (of
positive integers only)
Also: log_u, but seems to only accept one
argument, bsc, bcs, bct (again if you have information, I’d be greatful)
Storage variables: D, E, F
|
3rd
|
Trig:
sin^-1, cos^-1, tan^-1
Hyperbolic: sinh^-1, cosh^-1, tanh^-1
Other: degree and radian conversions, hypotenuse
function, √2, fractions of π
Storage variables: G, H, I
|
Rad
|
Length Conversions: in/mm, in/cm/ ft/m, gal/L, lb/kg, km/mi
Storage variables: M, N, O
|
5th
|
Linear Equations
|
2nd, 3rd
|
Combinations, permutations, factorials (of
positive integers only), temperature conversions between Celsius, Fahrenheit,
and Kelvin, random integers (dice, coin, deck of cards, from 1 to 10)
Also: [x-y], I don’t get this one either
Storage Variables: J, K, L
|
2nd, rad
|
Length Conversions: in/ft, ft/yd, yd/mi,
mm/cm, cm/m, m/km
Storage Variables: P, Q, R
|
2nd, 5th
|
Systems of Linear Equations, 2 x 2 and 3 x 3
|
3rd, rad
|
Cooking Conversions: tablespoons/teaspoons, tablespoons/cups,
cups/pints, pints/quarts, quarts/gallons/ teaspoons/milliliters
Storage Variables: S, T, U
|
3rd, 5th
|
Quadratic and Cubic Equations
|
Rad, 5th
|
Geometry:
spheres (.sp), circles (.c), trapezoids (/t), rectangles (.r),
triangles (Heron’s formula, .t), boxes (.b)
|
2nd, 3rd, rad
|
Mass Conversions: oz/lb, lb/tons, tons/l.t.,
g/kg, t/kg, ton/t (t is UK tons?, ton:
US tons)
Storage Variables: V, W, X
|
2nd, 3rd, 5th
|
Quartic Equations
Storage Variables: C, D, E
|
3rd, rad, 5th
|
Geometry:
cylinders (.cy), Cones (.co)
Finance:
payment of a loan or mortgage (.b), present value of an annuity (.p),
future value of an annuity (.f).
I have not figured out what the (.i) is for
(yet).
|
2nd, 3rd, rad, 5th
|
Storage Variables A-Z
|
Chain
Mode
The SciPro Math app does not follow the order
of operations, as we would expect. You
would note that none of these keyboards has
parenthesis. This means the operation
you press will have an effect on the number in the display.
For example, if you want to calculate (7 * 2) +
(16 * 5), you would have use the temporary memory keys, like so:
[mc] (to
clear memory)
7 [ * ] 2
[ = ] [m+]
16 [ * ] 5 [ = ] [m+]
[mr]
Result: 94
Another example: √((2^3 – 3)/(3^2 + 5)). Let’s use memory variables A and B this time,
with the no modifiers turn on.
2 [x^3] [ - ] 3 [ = ] [→Xv] [Av]
3 [x^2] [ + ] 5 [ = ] [→Xv] [Bv]
[Av] [ ÷ ] [Bv] [ = ]
Result:
0.5714285714286
Documentation
Despite having a website, on thing that this app
lacks is documentation. There is no
on-help facility. Their web page does
not have any details on the keys.
There are several keys on this app that I have
questions about like [sci], [bct], and [x-y] that I mentioned that I do know
what these functions are or how they work. If you do, please feel free to leave
some comments, it is much appreciated.
There are some tutorials on the SciPro Math’s
YouTube page, which I will document next.
Tutorials
The SciPro Math app has a YouTube which has the
following tutorials:
Quadratic Equations
Cubic Equations
Quartic Equations
I wish more videos were on this page (and
hopefully they will put more tutorials on the page in the future).
I’m going to discuss some of the features for
this App.
Hypotenuse Function
Modifiers: 3rd
The [hyp] function calculates the hypotenuse √(a^2
+ b^2). Syntax: a [hyp] b [ = ]
Example:
Calculate √(9^2 + 16^2)
Keystrokes:
9 [hyp] 16 [ = ]
Result:
18.3575597506858
CAUTION: I think the keys for [ a ], [ A° ], [ b ], [
B° ], and [ c= ] are supposed to be used for Pythagorean Theorem. With A° and B° are corresponding angles to
the sides with length a and b. However,
when I tested these keys, c, which I think represents the hypotenuse, I get
unexpected answers.
For example, if I entered a = 5 and b = 3, I
expect answer of c = √(5^2 + 3^2) = 5.83095189485. Instead, I get an answer of 8. (5 + 3).
Finance
Modifiers: 3rd, 4th (to rad), 5th
Notes:
*
Interest is entered as a decimal. For
example, enter 5% as 0.05.
*
Enter periodic interest rate, not annual interest. For monthly mortgages or payments, divide the
annual rate by 12. This is similar to
the HP 12C series or the classic BA 35.
* End-of-period payments are assumed.
At
the time of the review, there was not a lot documentation on the finance
section, I compared results with financial calculators to figure some of the
keys out.
Payment of a
Loan/Mortgage (Installment Buying)
Input:
Amount
of loan stored in A.b
Periodic
interest stored in i.b
Number
of periods stored in n.b
Output:
Press
[R.b=] for the payment
Example: Find the monthly payment of an auto loan with
$22,000 to be financed at 4% annual rate.
The term is 6 years.
Keystrokes:
22000
[→(X)v] [ A.b ]
0.04
[ ÷ ] 12 [ = ] [→(X)v] [ i.b ]
6
[ * ] 12 [ = ] [→(X)v] [ n.b ]
[R.b=]
Result: 344.194027595888
The
monthly payment is $344.19.
Present
Value of an Annuity (Annuity PV)
Input:
Periodic
payment stored in R.p
Periodic
interest stored in i.p
Number
of periods stored in n.p
Output:
Press
[A.p=] for the present value of the annuity
Example: What would an investor need to deposit if
the investor expects to have a $1,500.00 monthly payment, every month for the
next 30 years? The bank is expecting to
pay at a rate of 4.18% annual.
Keystrokes:
1500
[→(X)v] [R.p]
0.0418
[ ÷ ] 12 [ = ] [→(X)v] [i.p]
30
[ * ] 12 [ = ] [→(X)v] [n.p]
[A.p=]
Result: 307471.201192414
The
investor should deposit $307,471.20.
Future Value of an
Annuity (Annuity Amount)
Input:
Periodic
payment stored in R.f
Periodic
interest stored in i.f
Number
of periods stored in n.f
Output:
Press
[A.f=] to calculate the future value of the annuity
Example: An investor contributes $1,325.00 to a saving
fund that compounds monthly at a 4.08% annual rate. What will be the value of the annuity in 5
years?
Keystrokes:
1325
[→(X)v] [R.f]
0.0408
[ ÷ ] 12 [ = ] [→(X)v] [i.f]
5
[ * ] 12 [ = ] [→(X)v] [n.f]
[A.f=]
Result: 88024.3906860951
The
annuity is expected to have a value of $88,024.39 in 5 years.
CAUTION: I am not 100% sure of what the “.i” keys
calculate.
Systems
of Linear Equations
Modifiers: 2nd, 5th
This
keyboard is pretty much straight forward.
2
x 2 Systems:
a1
* x + a2 * y = a3
b1
* x + b2 * y = b3
The
[ D2*2 ] key calculates the determinant of the matrix [ [a1, a2], [b1, b2]
]. Store the values in to a1, a2, a3,
b1, b2, and b3 by using the [ →Xv ] key.
Solutions can be found by pressing the [ x2*2 ] and [ y2*2 ] keys
respectively.
Example:
Solve
the system:
4x
+ 2y = 1
-3x
+ 6y = -8
Keystrokes:
[reset]
4
[→(X)v] [ a1 ], 2 [→(X)v] [ a2 ], 1 [→(X)v] [ a3 ]
3
[(-)] [→(X)v] [ b1 ], 6 [→(X)v] [ b2 ], 8 [(-)][→(X)v] [ b3 ]
[
x2*2 ] returns 0.733333333…
[
y2*2 ] returns -0.966666666…
[
D2*2 ] returns 30 (determinant)
3 x 3 System:
a1 * x + a2 * y + a3 * z = a4
b1 * x + b2 * y + b3 * z = b4
c1 * x + c2 * y + c3 *z = c4
Input: [
a1 ] through [ c4 ] keys
Solutions:
[ x3*3 ], [ y3*3 ], [ z3*3 ]; with determinant [ D3*3 ]
Verdict
I really like what the SciPro Math app is going
for: app containing many solvers for
common problems in mathematics, and life.
I also like the wide variety of mathematical constants, it’s not every
day that a calculator has keys dedicated to ϕ, π/4, and √2.
The keys are nice size and the screen is
readable. The user may like a chain
operating system but it will take a little getting used to for a scientific calculator
app. The lack of parenthesis may be a
turn off for some users. Remember, this
is not an RPN calculator.
I would to see the angle mode become a separate
mode, not tied to a modifier. Having it
tied to a modifier key (4th) defeats the purpose of the angle mode. There is also an absence of settings (fixed,
engineering, scientific notation, not to mention, no scientific notation key).
If you are looking for statistical functions,
including regression analysis, this is not the app to find it.
The biggest problem I have is the lack of
documentation. This is a fairly young
app (November 2017), so I hope to see more documentation and the bugs worked
out in future revisions and updates. I
see the potential.
If you are interested, I would suggest getting
the app now (January 2018) for only $4.99 before it goes up to $9.99 in
February.
Eddie
This blog is property of Edward Shore, 2018.





