------------
Welcome to March Calculus Madness!
------------
frac(x): fractional part function
Domain: 0 ≤ frac(x) < 1
∫ frac(x) dx for x = 0 to 1
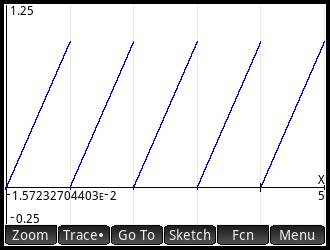
According to the graph above, the area between resembles as a right triangle.
When 0≤x<1, frac(x) = x
Hence:
∫ frac(x) dx for x = 0 to x = 1
Note:
lim a→1- (∫ frac(x) dx for x = 0 to x = a)
= lim a→1- (∫ x dx for x = 0 to x = a)
= lim a→1- (∫ x dx for x = 0 to x = a)
= lim a→1- (a^2/2 - 0)
= 1/2
What if the upper limit is less than 1?
Let b where, 0≤x≤b<1 (b<1):
∫ frac(x) dx for x = 0 to x = b
= ∫ x dx for x = 0 to x = b
= b^2/2
Eddie
All original content copyright, © 2011-2022. Edward Shore. Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited. This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author.