I hope you are all enjoying the day/night so far. The subject of Part 7 of the HP 39gii will be App-Specific commands.
We will work with app and global variables, as well as switching applications and doing App specific commands to our advantage. The two primary commands we will work with are STARTAPP and STARTVIEW.
STARTAPP and STARTVIEW
STARTAPP does what it advertises: starts the specific application called. The required application is stated as a string. For example, STARTAPP("Function") starts the Function graphing app. Running this command is key if you want the user to access specific screens, such as the Symbolic, Plot, and Numeric screens.
Keyboard sequence for STARTAPP is: [Shift] [Math] [ F1 ] [ 1 ] [ 2 ].
Applications include:
"Function" - Function Graphing
"Parametric" - Parametric Graphing
"Polar" - Polar Graphing
"Sequence" - Recurring Sequence Graphing
"Solve" - Solver Interface
"Triangle Solver" - Application for solving sides and angles of triangles
"Finance" - Time Value of Money Application
"Statistics 1Var" - 1 Variable Statistics
"Statistics 2Var" - 2 Variable Statistics
"Inference" - Hypothetical Testing and Confidence Intervals
"Linear Explorer" - Teaching application regarding linear equations
"Quadratic Explorer" - Teaching application regarding quadratic equations
"Trig Explorer" - Teaching application regarding trigonometric functions
"Data Streamer" - Application that works with Hewlett Packard's StreamSmart devices (data collection from various apparatus)
STARTVIEW leaves the user at a specific view, such as the Home screen, Plot screen, etc. Each screen has a specific view code, with syntax STARTVIEW(code). Some view codes are:
0: Symbolic Screen
1: Plot Screen
2: Numeric Screen
3: Symbolic Setup Screen
4: Plot Setup
5: Numeric Setup
6: App Information (accessed by [Shift] [Apps])
7: Views Key (same as if you pressed the [Views])
-1: Home Screen
-2: Mode Setup Screen
Keyboard sequence for STARTVIEW is: [Shift] [Math] [ F1 ] [ 1 ] [ 3 ].
App Variables
App variables are global. Some are specific to one app while others are applicable to several apps. I usually type of the variables, but you can find the app variables by pressing [Vars] [ F2 ]. The order of the apps shift, with the current app on top. I will present some app variables. This is not the extensive list by any means, so please check out the HP 39gii manual for a complete list.
App Variables Specific to One App
Function Symbolic - There are ten functions that are named F#, with # representing a digit 0 through 9. F1 is at top of the Symbolic view, F0 is at the bottom.
Parametric Symbolic - Similar to Function; names are X1 - X9, X0 and Y1 - Y9, Y0.
Polar Symbolic - Similar to Function; names are R1 - R9, R0
Sequential Symbolic - Similar to Function; names are U1 - U9, U0
Solve Symbolic - you can store ten equations in the solve variables E1 - E9, E0
You can store graphing expressions and equations to the appropriate variable by using a string around your expression/equation. You can use both methods of storing (store arrow and the equals-colon assignment syntax) Examples:
"SIN(X^2)" → F1 (store to Function F1)
E3 := "A^2 + B^2 = C^2" (store to Equation E3)
Statistics - 1 Variable:
Data: D1 - D9, D0 (lists)
Analysis: H1 - H5
Set the sample by the command SetSample(H#, D#);
Statistics - 2 Variable:
Data: C1 - C9, C0 (lists)
Analysis: S1 - S5
Set the data to be analyzed by the commands:
SetIndep(S#, C#);
SetDepend(S#, C#);
App Variables used by Several Apps
The Plot window: Xmin, Xmax, Ymin, Ymax, Xscl, Yscl, Tmin, Tmax, Tstep, θmin, θmax, θstep
Three ways to access θ:
1. Be in Polar mode and press [X,T,θ,N].
2. Echo θ from the Characters Menu: [Shift] [Vars] [ F2 ] [ 7 ] (Greek and Coptic) [ F4 ] (Page Down) [ left ] [ left ] [ up ] [ up ] [ F6 ] (OK)
3. char(952) returns "θ" while expr(char(952)) returns θ.
CHECK and UNCHECK
CHECK turns a certain equation/expression on. UNCHECK, as you probably guessed, turns named function off.
Syntax:
CHECK(n)
UNCHECK(n)
Just the number is accepted: n refers to the equation/expression listed in the current app. Despite what the manual says, CHECK (F1) produces an error, n must be numerical.
With that long intro done, let's get to the programming!
The Program SSAT (Simple Statistics)
SSAT takes a list, turns on the Statistics 1-Variable app, and returns:
* The number of elements in the list
* The mean
* The standard deviation
After the results are displayed, you are returned to the home screen.
Note: The commands SetSample and Do1VStats are found in then Command-App-Statistics 1 Variable menu. ([Shift] [Math] [ F2 ])
Program:
EXPORT SSTAT(D)
BEGIN
D1:=D;
STARTAPP("Statistics 1Var");
SetSample(H1,D1);
Do1VStats(H1);
PRINT();
PRINT("n="+Nbltem);
PRINT("Mean="+MeanX);
PRINT("SDev="+sX);
STARTVIEW(-1);
END;
Example:
SSTAT({3,4.5,4.4,4.6,4,3.9,3.8,3,3.2}) returns
n=9
Mean=3.822222222
SDev=.630035272381
The Program PLOTF
The program PLOTF takes three arguments.
PLOTF(function of X as a string, left limit, right limit)
The function F0 is turned on while the other functions F1 - F9 are turned off. The Function app is tuned on the program terminates at the plot screen.
Program:
EXPORT PLOTF(f,a,b)
BEGIN
LOCAL c,d,K;
STARTAPP("Function");
Xmin:=a;
Xmax:=b;
c:=0;
d:=0;
f → F0(X);
CHECK(0);
FOR K FROM 1 TO 9 DO
UNCHECK(K);
END;
FOR K FROM a TO b STEP (b-a)/256 DO
IF F0(K) < c THEN
c:=F0(K); END;
IF F0(K) > d THEN
d:=F0(K); END;
END;
Ymin:=c-1;
Ymax:=d+1;
Xtick:=10^(ROUND(LOG(b-a),0));
Ytick:=10^(ROUND(LOG(d-c),0));
STARTVIEW(1);
END;
Example: Plot y = 2x^3 - x + 0.5 from -5 ≤ x ≤ 5
PLOTF("2X^3-X+0.5",-5,5) gets this:
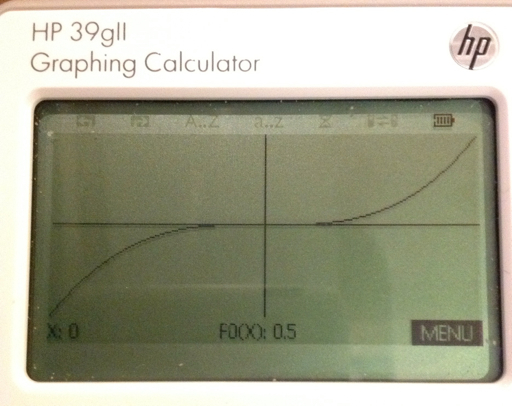
The Program PROJECTILE
PROJECTILE does the following:
1. Switch the 39gii to the Parametric app and Degrees mode
2. Determines the projectile's range and height. No air resistance is assumed. You determined whether you are working in: SI (meters) or US (feet).
3. The path of the projectile is graphed.
Input: PROJECTILE(initial height, initial velocity, initial angle in degrees)
The program will ask you to select the value of the gravitational constant:
g = 9.80665 m/s^2
Or
g = 32.17405 ft/s^2
Program:
EXPORT PROJECTILE(y0, v0, a0)
BEGIN
LOCAL K;
STARTAPP("Parametric");
CHOOSE(K,"g=","9.80665 m/s²","32.17405 ft/s²");
IF K==0 THEN KILL; END;
IF K==1 THEN G:=9.80665; END;
IF K==2 THEN G:=32.17405; END;
HAngle:=1;
I:=y0;
V:=v0;
A:=a0;
"V*COS(A)*T" → X0(T);
"I+V*SIN(A)*T-0.5*G*T²"→Y0(T);
CHECK(0);
FOR K FROM 1 TO 9 DO
UNCHECK(K); END;
W:=FNROOT(Y0(T)=0,T,10);
R:=X0(W);
S:=FNROOT(X0(T)=R,T,10);
H:=(V²*(SIN(A))²)/(2G);
Xmin:=0;
Xmax:=R+2;
Ymin:=-1;
Ymax:=H+2+I;
Tmin:=0;
Tmax:=S;
Tstep:=S/240;
MSGBOX("Range: "+R);
MSGBOX("Height: "+H);
STARTVIEW(1);
END;
Example:
Initial height=2.1 ft
Initial velocity=56.5 ft/s
Initial angle=46.76°
PROJECTILE(2.1,56.5,46.7), select g=32.17405 ft/s^2
Results: (in feet)
Range: 100.984422673
Height: 26.2756069802
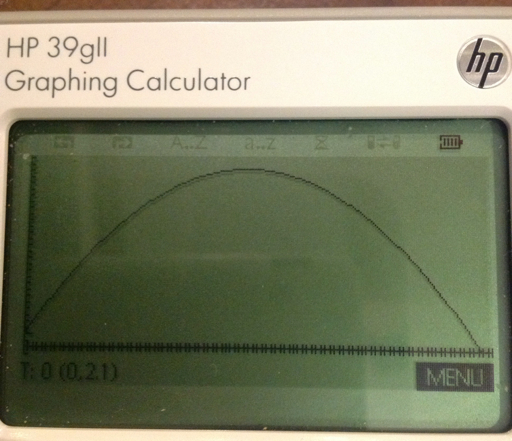
This concludes Part 7 of the HP 39gii programming tutorial. Until next time,
Eddie
Have a great day! Much happiness!
This blog is property of Edward Shore. 2013


























