It's 2014 Somewhere!

In these 24 hours, a new year will begin. Here is to a happy, healthy, and successful 2014. Cheers!

Eddie

HP Prime: Drawing Pixelated Pictures (DRAWICON4, DRAWICON6)

Drawing Iconic Pictures with the HP Prime

4 x 4 Pixels: DRAWICON4(number)

Entry: Real number, integer

The number is ultimately converted into a binary number, with each of the 16 bits fitting a 4 x 4 matrix. If the square is turned "on" (having a value of 1), a square will be drawn. Each space if the matrix represents a binary bit: 2^0, 2^1, 2^2, 2^3, etc. The lowest value bit is located at the bottom, right-hand corner element of the matrix.

You can specify whether the squares will be drawn in black or a specific color. The 4 x 4 matrix of bits is represented as this:

[ [ 2^15, 2^14, 2^13, 2^12 ],
[ 2^11, 2^10, 2^9, 2^8 ],
[ 2^7, 2^6, 2^5, 2^4 ],
[ 2^3, 2^2, 2^1, 2^0 ] ]

Program:

Comments followed by // are for notes and do not necessarily have to be typed.


EXPORT DRAWICON4(m)
BEGIN
// EWS 12/28/2013

// does the user want color?
LOCAL ch, R, G, B;
CHOOSE(ch,"Color?","Black","Yes");
IF ch==1 THEN
ch:=RGB(0,0,0);
ELSE
INPUT({R,G,B}, "Color Input",
{"Red","Green","Blue"},{ },{0,0,0});
ch:=RGB(R,G,B);
END;

// convert m to real to be broken down
// Type 1 is an integer (#)
IF TYPE(m)==1 THEN
m:=B→R(m);
END;

// remove negation and fraction parts (so entries like -12 and 34.55 are acceptable)
m:=ABS(IP(m));

// allow m to be text by storing it in M
LOCAL M:=m;

// check for upper limit
IF m>65535 THEN
MSGBOX("Excess of 65535!");
KILL;
END;

// break m into its binary parts and puts them in the required order
LOCAL n:=15,r,c,
mat:=MAKELIST(0,X,1,16);

REPEAT
IF 2^n≤m THEN
m:=m-2^n;
mat(n+1):=1;
END;
n:=n-1;
UNTIL n<0;
mat:=REVERSE(mat);

// list2mat(list, number of columns) - found in the catalog
mat:=list2mat(mat,4);

// drawing a border and label
RECT();
RECT_P(129,79,189,139,RGB(0,0,255),
RGB(255,255,255));
TEXTOUT_P(M,139,0,4,RGB(0,128,0));

// use the matrix to draw the squares
// pixels x = columns, y = rows
FOR r FROM 1 TO 4 DO
FOR c FROM 1 TO 4 DO

IF mat(r,c)==1 THEN
RECT_P(129+15*(c-1), 79+15*(r-1),
129+15*c, 79+15*r, ch);
END;
END;
END;

WAIT(0);

END;

Here is a 6 x 6 version:

DRAWICON6

6 x 6 Pixels: DRAWICON6(number)

Entry: Real number, integer

The program is an almost carbon-copy of DRAWICON4, except the limits have changed.


Program:

Comments followed by // are for notes and do not necessarily have to be typed.

EXPORT DRAWICON6(m)
BEGIN
// EWS 12/28/2013

// does the user want color?
LOCAL ch, R, G, B;
CHOOSE(ch,"Color?","Black","Yes");
IF ch==1 THEN
ch:=RGB(0,0,0);
ELSE
INPUT({R,G,B}, "Color Input",
{"Red","Green","Blue"},{ },{0,0,0});
ch:=RGB(R,G,B);
END;

// convert m to real to be broken down
// Type 1 is an integer (#)
IF TYPE(m)==1 THEN
m:=B→R(m);
END;

// remove negation and fraction parts (so entries like -12 and 34.55 are acceptable)
m:=ABS(IP(m));

// allow m to be text by storing it in M
LOCAL M:=m;

// check for upper limit
IF m>2^36-1 THEN
MSGBOX("Excess!");
KILL;
END;

// break m into its binary parts and puts them in the required order
LOCAL n:=35,r,c,
mat:=MAKELIST(0,X,1,36);

REPEAT
IF 2^n≤m THEN
m:=m-2^n;
mat(n+1):=1;
END;
n:=n-1;
UNTIL n<0;
mat:=REVERSE(mat);

// list2mat(list, number of columns) - found in the catalog
mat:=list2mat(mat,6);

// drawing a border and label
RECT();
RECT_P(129,79,219,169,RGB(0,0,255),
RGB(255,255,255));
TEXTOUT_P(M,139,0,4,RGB(0,128,0));

// use the matrix to draw the squares
// pixels x = columns, y = rows
FOR r FROM 1 TO 6 DO
FOR c FROM 1 TO 6 DO

IF mat(r,c)==1 THEN
RECT_P(129+15*(c-1), 79+15*(r-1),
129+15*c, 79+15*r, ch);
END;
END;
END;

WAIT(0);

END;

Have fun and thank you as always!

I wonder how much of a challenge to do this on a TI-84?

See you next time!

Eddie


This blog is property of Edward Shore. 2013

Season Greetings!

Greetings! Thank you everybody for making this blog as successful as it is. Look for more exciting things to come into 2014. Merry Christmas and have a happy holiday season!

Eddie

This blog is property of Edward Shore. 2013

HP Prime: CAS Commands in Home Mode

(Common) CAS Commands in Home Mode

(udpated 4/17/2014)

Two things to aware of:

1. Any command from the CAS mode to be used in the Home Mode, regardless of entry, must have a "CAS." prefix. Examples include CAS.diff, CAS.simplify, etc.
2. Algebraic (symbolic) objects need single quotes surrounding them. They can be called by pressing Shift+Parenthesis Key ().
3. Not all CAS commands work as expected in Home and Programming. My focus is on the Home mode.

---

Simplify: CAS, 1, 1

Syntax:
Non-RPN: CAS.simplify('expression')
RPN: Not recommended - as it will numerically evaluate the expression

---

Expand: CAS, 1, 3

Syntax: CAS.expand('expression')
RPN: Not recommended - as it will numerically evaluate the expression

Example: CAS.expand('(X+3)^2') returns X^2+6*X+9

---

Factor
There are two commands for factoring:

Polynomial: CAS.Factor: CAS, 1, 4
Non-RPN Syntax: CAS.factor('expression')
Example: CAS.Factor('X^2-5*X+4') returns (X-4)*(X-1)

Integer: CAS.ifactor: CAS, 5, 2
Non-RPN Syntax: CAS.ifactor(integer)
Example: CAS.ifactor(186) returns 2*3*31

RPN Syntax:
1: integer
CAS.ifactor(1), press Enter

---

Differentiation: CAS, 2, 1
Non-RPN Syntax: CAS.diff('expression')

Simplification may be needed. So call up CAS.simplify, put up single quotes using Shift+Parenthesis Key, key up to the expression, press Copy (soft key), then press Enter

Example:
CAS.diff('COS(X)*SIN(X)') returns -SIN(X)*SIN(X)+COS(X)*COS(X)
CAS.simplify('-SIN(X)*SIN(X)+COS(X)*COS(X)') returns 2*COS(X)^2-1

RPN Syntax:
1: 'f(X)'
CAS.diff(1), press Enter

Update (4/17/2014):  If the above does not work, try this syntax:

CAS.diff('expression', 'variable')  

Example:  CAS.diff('COS(X)*SIN(X)', 'X') returns  -SIN(X)*SIN(X)+COS(X)*COS(X)






RPN:
2:  'expression'
1:  'variable'
CAS.diff(2), press enter

---

Integration: CAS, 2, 2
Non-RPN Syntax: CAS.int('expression')

Simplification may be needed. So call up CAS.simplify, put up single quotes using Shift+Parenthesis Key, key up to the expression, press Copy (soft key), then press Enter

Example:
CAS.int('2*e^(4*X)') returns 2*e^(4*X)/4
CAS.simplify('2*e^(4*X)/4') returns e^(4*X)/2

Not recommended for RPN Entry





Update (4/17/2014):  If the above syntax does not work, try:



CAS.int('expression', 'variable')

Example:  
CAS.int('2*X*e^(4*X)','X') returns 2*(4*X-1)/16*e^(4*X)
CAS.simplify('2*(4*X-1)/16*e^(4*X)') returns (4*X*e^(4*X) - e^(4*X))/8

---

Summation (Σ): CAS, 2, 5
Non-RPN Syntax: CAS.sum('expression', 'variable', start, end)
Example: CAS.sum('N^3','N',1,9) returns 2025

RPN Syntax:
4: 'expression'
3: 'variable'
2: start
1: end
CAS.sum(4) press Enter

Note: Start and End must be numerical limits.

---

Solving

I recommend zeros and cZeros, not solve and cSolve. The syntax is pretty much the same.

Access:
zeros: CAS, 3, 2
cZeros: CAS, 3, 4

If the equation is f(X) and we are solving for X:

Non-RPN Syntax: CAS.zeros('f(X)')

RPN Syntax:
1: 'f(X)'
CAS.zeros(1), press Enter

Example:
CAS.zeros('X^3-6') returns [1.81712059283]

If you are solving for variables other than X:

Non-RPN Syntax: CAS.zeros('expression', 'variable')

RPN Syntax:
2: 'expression'
1: 'variable'
CAS.zeros(2), press Enter

Got to include the variable!

Example:
CAS.zeros('R^3-6') returns [].
CAS.zeros('R^3-6','R') returns [1.81712059293]


Hope this helps and we will cover more of this subject in the future.

Eddie

This blog is property of Edward Shore. 2013

Modular Arithmetic: Basics and Solving x MOD A = B and A MOD x = B (with A ≥ 0 and B ≥ 0)

Good to talk with you all again. Before we get back to HP Prime programming goodness, let's make a side trip into algebra land.

The Modulus Function

Definition:

X MOD Y = R where

R = remainder(X/Y) = frac(X/Y) * Y

A practical way to get the modulus is to get the remainder (in other words, what's left over) of the division X/Y.

For example:

13 MOD 5 = 3

Divide 13 by 5, we get the quotient of 2 and the remainder of 3.

Properties:

Let A and B be integers.

A MOD A = 0. Easily justified since an integer divided by itself has no remainder.

If B > A, A > 0, and B > 0, then A MOD B = A. Any integer divided by a larger integer, the remainder will be an original integer.

Example: 11 MOD 12 = 11. The division of 11/12 has the quotient of 0 and the remainder of 11.

A common way to think of the modulus function is dealing clocks and calendars (MOD 12).

x MOD A = B, A ≥ 0 and B ≥ 0

General solution: x = B + A*n, where n is any integer

Example:
x MOD 4 = 2.

Easily x = 2 is a solution since 2/4 leaves a quotient of 0 and remainder of 2.

Observe that x = 6 also works. 6/4 has a quotient of 1 and a remainder of 2.

Hence the solution is: x = 2 + 4 * n

A MOD x = B, A ≥ 0 and B ≥ 0

A way to find possible solutions is to build a table, using the good old trial and error technique. Stop when we get to A MOD A. (See the Properties section above) This can get very lengthy when A gets large. In trade, you can easily see the solutions of A MOD x = B (if solutions exist).

Example 1: 11 MOD x = 3

11 MOD 1 = 0
11 MOD 2 = 1
11 MOD 3 = 2
11 MOD 4 = 3
11 MOD 5 = 1
11 MOD 6 = 5
11 MOD 7 = 4
11 MOD 8 = 3
11 MOD 9 = 2
11 MOD 10 = 1
11 MOD 11 = 0

From this we find that the solutions are x = 4 and x = 8. A very fortunate occasion.

Example 2: 13 MOD x = 8

13 MOD 1 = 0
13 MOD 2 = 1
13 MOD 3 = 1
13 MOD 4 = 1
13 MOD 5 = 3
13 MOD 6 = 1
13 MOD 7 = 6
13 MOD 8 = 5
13 MOD 9 = 4
13 MOD 10 = 3
13 MOD 11 = 2
13 MOD 12 = 1
13 MOD 13 = 0

Darn it! No solution to 13 MOD x = 8. It happens sometimes.


Hopefully this is helpful. Thank you for your comments and questions. Honestly I can't thank you enough. Have a great day!

Eddie


This blog is property of Edward Shore. 2013

HP Prime Programming Tutorial #8: ARC, LINE, and Placement of Graphics

Welcome to Part 8 of the HP Prime Tutorial. Continuing in our drawing commands, we are going to feature ARC and LINE.

ARC and ARC_P: Draws a Circle or a Circular Arc

Syntax:

Cartesian:
ARC(x, y, r, angle 1*, angle 2*, color*).

Pixels:
ARC_P(x, y, r, angle 1*, angle 2*, color*)

x: x coordinate

y: y coordinate

r: length of the radius in pixels. This is why I prefer using pixel commands in my programming.

angle 1 and angle 2: If included, these two arguments draw an arc segment. The angle follows the conventional circle notation, starting with 0 (due east) going counter clockwise. Use the current angle mode.

color: color of the arc. To use it, angle 1 and angle 2 must be included.

LINE and LINE_P

Draws a line segment from (x1, y1) to (x2, y2). The color is optional.

Syntax:

Cartesian:
LINE(x1, y1, x2, y2, color*)

Pixels:
LINE_P(x1, y1, x2, y2, color*)

The next to programs CIRCLE1 and CIRCLE2 do the same thing: draw a circle, label quadrants and angels. The reason why I am posting these two is that when you are programming graphics, care must be given. Adjustments to where graphics are placed can be necessary and I hope CIRCLE1 and CIRCLE2 illustrates this.

Medium font is assumed (set in Home Settings).

The angle symbol (°) get be retrieved by pressing Shift + 9 and selecting ° from the grid.

CIRCLE1 (the "rough draft", if you will):

EXPORT CIRCLE1()
BEGIN
RECT();
TEXTOUT_P("Circle", 0, 0);
TEXTOUT_P("II",109,59);
TEXTOUT_P("90°",159,59);
TEXTOUT_P("I",209,59);
TEXTOUT_P("180°",109,109);
TEXTOUT_P("0°",209,109);
TEXTOUT_P("III",109,159);
TEXTOUT_P("270°",159,159);
TEXTOUT_P("IV",209,159);

LINE_P(0,109,318,109,RGB(16,16,16));
LINE_P(159,0,159,239,RGB(16,16,16));

ARC_P(159,109,30);
FREEZE;
END;

The results:

This is good, but we can do better. First I am going to move the labels II, 180°, and III 10 pixels to the left, primarily so the 180° label does not touch the circle.

Second I am going to move the labels III, 270°, and IV up 10 pixels to make the bottom line look better and not "so far away" from the circle.

Although it is not necessarily, I am going to make the angle labels blue. I will need to specify the font size code at 0.

Finally, I find that the lines are too dark. I am going to make them a bit more gray.

Here is the second revision. For the purposes of this tutorial, I call this program CIRCLE2. All changes are in bold.

EXPORT CIRCLE1()
BEGIN
RECT();
TEXTOUT_P("Circle", 0, 0);
TEXTOUT_P("II",99,59);
TEXTOUT_P("90°",159,59,0,RGB(0,0,255));
TEXTOUT_P("I",209,59);
TEXTOUT_P("180°",99,109,0,RGB(0,0,255));
TEXTOUT_P("0°",209,109,0,RGB(0,0,255));
TEXTOUT_P("III",99,149);
TEXTOUT_P("270°",159,149,0,RGB(0,0,255));
TEXTOUT_P("IV",209,149);

LINE_P(0,109,318,109,RGB(128,128,128));
LINE_P(159,0,159,239,RGB(128,128,128));

ARC_P(159,109,30);
FREEZE;
END;

A better looking picture.

As always, thanks for your time, comments, and questions. Hopefully this session is helpful.


This blog is property of Edward Shore. 2013


Eddie

** Note: Thanks to Dennis for pointing out my typo.  It is corrected now.  3/5/2014

 

HP Prime Programming Tutorial #7: TEXTOUT

Greetings everyone. It has been too long since I last posted. I hope everyone had a fantastic Thanksgiving. For those of you who are battling cold and stormy weather, please be safe. For those of you living in the Southern Hemisphere where summer is about to begin... I'm jealous! :) I love summer.

Introduction

OK this section we will start covering some of the graphics features of the HP Prime Programming Language. We touched on graphics a bit when we used STARTAPP and STARTVIEW to call up the Plot screen of certain apps (Function, Parametric, Polar, Advanced Grpahing).

This time we are going to use drawing commands that can be used in any HP Prime app. In a sense we are creating a graphic object (GROB). The HP Prime allows for ten graphic objects, named G0 - G9. For this tutorial series, (unless specified) I am always going to use the default GROB, G0. This makes typing commands much easier.

Cartesian vs Pixel

Each graphic object operates in either one of two coordinate systems: Cartesian and pixel. If you worked with the Hewlett Packard HP 39gii calculator, this might look familiar to you.

The features of the Cartesian system (x,y) are these:

* The end points depend on the Plot variables Xmin, Xmax, Ymin, and Ymax.
* The system is familiar, having x increasing as we move to the right and y increasing as we move up. (no shocker there).
* The trade is that some (very few) drawing commands don't accommodate the Cartesian system. An example is the ARC command, which requires the radius to be in pixels.

Below is a map of the Cartesian system:

The Pixel System (x,y):

* The boundaries are fixed. The pixel (0,0) is the top left hand corner, the pixel (318, 218) is the lower right hand corner.
* The value of x still increases as we go to the right. However, y increases as we go down, opposite of the Cartesian system. On the other hand, x and y are always non-negative.

The Drawing Commands

The HP Prime has two sets of drawing commands: one for the Cartesian system and one for the Pixel system. All commands for the Pixel system will have a "_P" suffix attached. For example:

LINE draws a line using Cartesian coordinates, while LINE_P draws a line using Pixel coordinates.

General Access: (in the Programming Editor)

Drawing Commands for the Pixel system: Cmds, 2. Drawing, 6. Pixels
Drawing Commands for the Cartesian system: Cmds, 2. Drawing, 7. Cartésian

Clearing the GROB screen

To clear the GROB screen, we will simply type RECT(). The wipes the screen, leaving it white. It is necessary to do this at least at the beginning of each program containing drawing commands. In a sense, RECT() is similar to PRINT().

---

Hint: To paint an entire screen a specific color, use RECT(color).

---

Showing the Graphics Screen

It is not enough to type the drawing commands. We need a command to tell the HP Prime to show the graphics. Two ways to do it are:

FREEZE: This does exactly what it says, freezes the screen. To exit, tap the screen or press ESC. Pressing Enter will re-execute the program.

Access: Cmds, 2. Drawing, 3. FREEZE

WAIT(0): This freezes the screen for an indefinite amount of time. However, pressing any button will cause the program to continue. Of course, if the last END is followed by WAIT(0), the program terminates.

Of course, you can use WAIT(n) to make the calculator wait n seconds before executing the next step.

TEXTOUT and TEXTOUT_P

TEXTOUT and TEXTOUT_P inserts text on a graphics object using Cartesian and Pixel coordinates, respectively. They are also at the bottom of the Cartesian and Pixel Drawing sub menus, respectively. (Use either the x,t,θ,n button or the up button followed by Enter).

Full Syntax (starred commands are optional):

Cartesian:
TEXTOUT(text, GROB*, x, y, font size*, text color*, width*, background color*)

Pixel:
TEXTOUT_P(text, GROB*, x, y, font size*, text color*, width*, background color*)

text: The text to be written. It can be a string, results, calculations, or any combination.

GROB*: Graphic Object G0 through G9 to be used. If left out, G0 is used.

x: x coordinate

y: y coordinate

font size*: The text font's size code. Must be used if you want text to be a color other than black. Optional. Default is the current size set by Home Settings.
0: Current font size as set by Home Settings screen.
1: Size 10 font
2: Size 12 font
3: Size 14 font
4: Size 16 font
5: Size 18 font
6: Size 20 font
7: Size 22 font

text color*: The color of the text. Use of the RGB command is advised. Optional. Default color is black.

width*: Length of the background box of the text. Optional. I usually don't use this argument.

background color*: Color of the background box. Optional. I usually don't use this argument.

Simplified Syntaxes:

Black text at default font size:
TEXTOUT(text, x, y)
TEXTOUT_P(text, x, y)

Colored text at a set font size:
TEXTOUT(text, x, y, size code, color)
TEXTOUT_P(text, x, y, size code, color)

With all this, we finally get to some programming. Since it is December, and snowing in a lot of the northern side of Earth, let's use TEXTOUT_P to draw snowflakes. I am going to use symbolize the snowflake by the asterisk, the symbol of multiplication in programming. [ × ] types *.

---

SNOWFLAKE

SNOWFLAKE takes one argument, which is the number of snowflakes to be drawn.

Note: Take note the order of the commands. The order regarding where to draw and generate random numbers is important to get the results you want.

Program:

EXPORT SNOWFLAKE(N)
BEGIN
LOCAL X,Y,Z,I,L0;
L0:={RGB(0,0,255),RGB(178,255,255),
RGB(30,144,255),RGB(0,255,255)};
\\ blue, light blue, dodger blue, cyan

RECT();

FOR I FROM 1 TO N DO
X:=RANDINT(0,304); \\ save some room since text takes pixels
Y:=RANDINT(0,208);
Z:=RANDINT(1,4);
Z:=L0(Z);
TEXTOUT_P("*",X,Y,2,Z);
END;

FREEZE;
END;

Next time - we will work with ARC and LINE. Until then, Happy Day/Evening everyone!


Eddie

This blog is property of Edward Shore. 2013

And in 25 days, it will be 2014!

ATAN2 using tan^-1 and angle/ARG (Various Calculators)

ATAN2

The function atan2(y,x) is defined as:

atan2(y,x) = tan^-1 (y/x) with respect to the quadrant the point (x, y) is in. In case you didn't know, with respect to point (x, y):

(x, y) is in Quadrant I if x > 0 and y > 0
(x, y) is in Quadrant II if x < 0 and y > 0
(x, y) is in Quadrant III if x < 0 and y < 0
(x, y) is in Quadrant IV if x > 0 and y < 0

Visually:

This is different from the two common calculator functions used to find the arctangent: Arctangent and Argument.

The Arctangent Function

TI and Casio Calculators*: tan^-1(y/x)
Hewlett Packard Calculators*: atan (y/x)

* The majority of them

Range (Output): -90° to 90°, -π/2 to π/2 radians

How to use Arctangent to get atan(y,x)

If the point is in quadrant I:
Use atan(y/x)

If the point is in quadrant II or III:
Use atan(y/x) + 180° in degrees mode
Use atan(y/x) + π in radians mode

If the point is in quadrant IV:
Use atan(y/x) + 360° in degrees mode
Use atan(y/x) + 2*π in radians mode

Special cases have to be used x or y is equal to 0:

If x=0 and y<0, the angle is 270° (3*π/2 radians)
If x=0 and y>0, the angle is 90° (π/2 radians)
If y=0 and x<0, the angle is 180° (π radians)
If y=0 and x>0, the angle is 360° or 0° (2*π or 0 radians)


The Argument Function

The complex number x + yi is used.

TI Calculators: angle(x + y*i)
Casio and Hewlett Packard Calculators: ARG(x + y*i)

Range: -180° to 180°, -π to π radians

How to use the Argument function to get atan2(y,x)

This is a great way to get atan2, which cleverly makes the use of complex numbers. In addition, there are a lot fewer things to remember:

If y≥0 (Quadrants I and II):
Use ARG(x+yi)*

(*The angle function if you are using a TI calculator)

If y<0 (Quadrants III and IV):
Use ARG(x+yi) + 360° for degrees mode
Use ARG(x+yi) + 2*π for radians mode


I hope this tip is helpful. Happy Thanksgiving and I am very thankful for all who have read, followed, and supported my blog over the last two years.

Eddie

This blog is property of Edward Shore. 2013

HP Prime Programming Tutorial #6: Subroutines

Subroutines

This session will show how routines work in HPPL. Generally, subroutines have be declared before the main program. Declaration is important. The details of the subroutines are after the main program.

Definitely take a look at the example programs to get a better understanding.

SUB Routines for HP Prime

General Syntax:

sub(); //declare subroutines

EXPORT main()
BEGIN
commands go here, including sub()
END;

sub()
BEGIN
commands go here
END;

---

SUBEXAM

This is just a demonstration of how sub routines work. This program calculates one of two values:

If A is positive, then the program evaluates A. If not, the program values B instead. Where:

A = 2(x-y)/Φ + xy
B = Φ^2

and Φ = 2e^(x+y) - e^(x-y) - e^(y-x)

We will use Φ as the subroutine.

SUB1();

EXPORT SUBEXAM(X,Y)
BEGIN
LOCAL A, B;
A:=(2*(Y-X))/SUB1(X,Y)+X*Y;
B:=(SUB1(X,Y))^2;
IF A>B THEN
RETURN A;
ELSE
RETURN B;
END;
END;

SUB1(X,Y)
BEGIN
RETURN 2*e^(X+Y)-e^(X-Y)-e^(Y-X);
END;

Examples:

SUBEXAM(-4, 1) returns 21998.918189
SUBEXAM(2,3) returns 86283.2797974
SUBEXAM(-5,-6) returns 30.648061288
SUBEXAM(2,-3) returns 21810.6046664

---

Days Between Dates

DDAYS Using Subroutines for HP Prime: Best for 1901 to 2099

* Remember century years not divisible by 400 are NOT leap years. This program does not take this into account. If any such years are passed, subtract one day for such year manually.

Source: HP 12C Manual - Hewlett Packard

// Declare Subroutines
SUB1();
SUB2();
SUB3();

// Main program
EXPORT DDAYS(m1,d1,y1,m2,d2,y2)
BEGIN
// ΔDYS HP 12C
LOCAL x1, x2, z1, z2;
x1:=SUB1(m1); x2:=SUB1(m2);
z1:=SUB2(m1,y1); z2:=SUB2(m2,y2);
RETURN SUB3(y2,m2,d2,z2,x2)-
SUB3(y1,m1,d1,z1,x1);
END;

SUB1(X)
BEGIN
IF X≤2 THEN
RETURN 0;
ELSE
RETURN IP(.4*X+2.3);
END;
END;

SUB2(X,Y)
BEGIN
IF X≤2 THEN
RETURN Y-1;
ELSE
RETURN Y;
END;
END;

SUB3(Y,M,D,Z,X)
BEGIN
RETURN 365*Y+31*(M-1)+D+IP(Z/4)-X;
END;
(Thanks to Owitte for pointing out my typo)


Examples:
Days Between Dates:

7/3/1985 to 2/28/1995 is 3,527 days

3/14/1977 to 11/17/2013 is 13,397 days

12/10/2010 to 6/30/2014 is 1,298 days

1/5/2015 to 3/19/2227 returns 77,506 BUT this program treats 2100 and 2200 as leap years, which in reality they are not. Subtract 2 to get the correct answer of 77,504 days.

So that is how subroutines work. Please give comments, ask questions, and always thanks to my supporters and readers. Cheers!

Eddie

This blog is property of Edward Shore. 2013

HP Prime Programming Tutorial #5: STARTAPP, STARTVIEW, RGB

Today's session is about starting other apps in a program and using colors.

---

Defining equations in the Program Editor and Home

The equation must be a string and be stored to the appropriate designated variable.

F# is for functions of X. (Function app).
R# is for polar functions of θ. (Polar app).
U# is for sequences of N, N-1, N-2. (Sequence app).
X# and Y# for parametric equations of T. (Parametric App)
V# for open statements and equations in the Advanced Graphing App, which The independent variables are X and Y.

# is a digit 0-9.

Defining equations this way leaves them uncheck. If you want them plotted or accessed in Num View, you will need to check them.

Example:
F1:="2*X^3" stores the function f(x) = 2*x^3 in Function 1.

R5:="A*SIN(θ)" stores the polar function r(θ) = A*sin(θ) in Polar Function 5, with A being what value stored in it.

---

STARTAPP

STARTAPP(application name in quotes);

Starts the named App. The calculator points the screen to the default view (Plot, Symb, Num).

Access: Cmds, 4. App Functions, 2. STARTAPP

---

CHECK and UNCHECK

Checks and unchecks specific equation or function (0-9) in the current app. For example, if you are in the Function app, CHECK(1) activates F. As you should expect, UNCHECK(1) turns F1 off.

What does CHECK and UNCHECK affect?
1. Whether a function is plotted in Plot view.
2. Whether a function is analyzed in Num view.

Access for CHECK: Cmds, 4. App Functions, 1. CHECK
Access for UNCHECK: Cmds, 4. App Functions, 4. UNCHECK

---

STARTVIEW

Instructs the HP Prime to go to a certain view. It has two arguments, the view number and a redraw number.

Common view numbers include (not all inclusive):
-2 = Modes screen
-1 = Home
0 = Symbolic (Symb)
1 = Plot
2 = Numeric (Num)
3 = Symbolic Setup
4 = Plot Setup
5 = Numeric Setup
6 = App Information
7 = The Views Key
8 = first special view
9 = second special view
Etc..

The redraw number is either 0 or non-zero. 0 does not redraw the screen, anything else does. I recommend the latter.

Syntax: STARTVIEW(view number, redraw number)

Access: Cmds, 4. App Functions, 3. STARTVIEW

---

RGB

Returns an integer code pertaining to a color's RGB code. This is super useful for drawing and text writing.

Syntax: RGB(red, green, blue, alpha)

Red: Intensity of Red, 0-255
Green: Intensity of Green, 0-255
Blue: Intensity of Blue, 0-255
Alpha: (optional) Opacity (up to 128).

RGB codes:
Blue: RGB(0,0,255)
Violet: RGB(143,255,0)
Dark Green: RGB(0,128,0)
Orange: RGB(255,127,0)
Yellow: RGB(0,255,255)
Red: RGB(255,0,0)
White: RGB(255,255,255)
Black: RGB(0,0,0)
Gray: RGB(129,128,128)
Brown: RGB(150,75,0)
Light Blue: RGB(173,216,330)

For other colors, RGB can be found on various sites on the Internet, including Wikipedia.

Access: Cmds, 2. Drawing, 5. RGB

---

Tip: Change a color of a graph

Use the syntax

F#(COLOR):=RGB(red,blue,green,[alpha]);

F stands for the designated function type (F for function, R for polar, etc)
# is the digit 0-9.

Example:
F8(COLOR):=RGB(0,0,255)
makes the function F8 plot in blue.

---

This is a lot, but this is doable. Let's see all these commands and tips in action and create some magic.

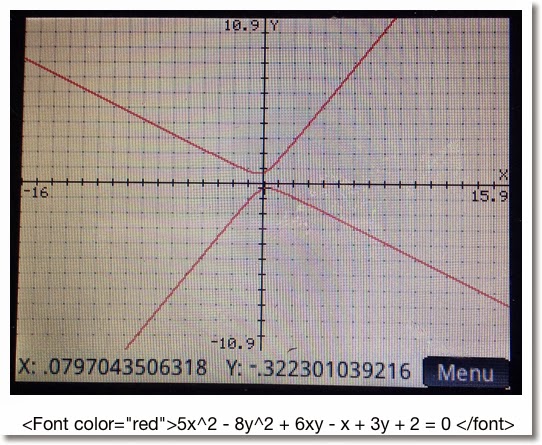
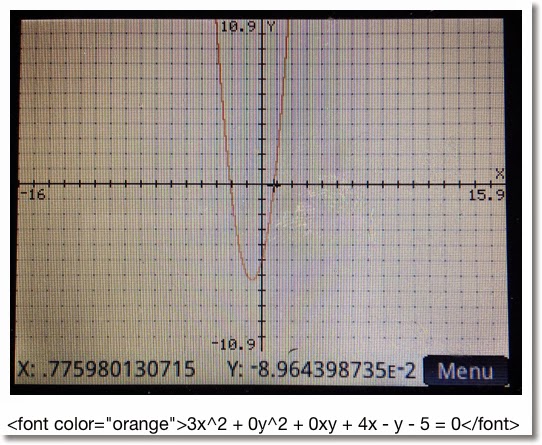
Conic Drawing for HP Prime

Draws the conic section for the general equation

Ax^2 + By^2 + Cxy + Dx + Ey + F = 0

You can choose the color how the conic section is plotted, from red, blue, orange, and green. (Game show enthusiasts take note of the order of the colors I listed... ;) ).

EXPORT CONIC()
BEGIN
LOCAL cr, cg, cb, I;
INPUT({A,B,C,D,E,F},
"Ax^2+By^2+Cxy+Dx+Ey+F", { }, { },
{0,0,0,0,0,0});

// Colors
CHOOSE(I, "Choose a Color",
"Red","Blue","Orange","Green");
cr:={255,0,255,0};
cg:={0,0,127,255};
cb:={0,255,0,0};

STARTAPP("Advanced Graphing");
V1:="A*X^2+B*Y^2+C*X*Y+D*X+E*Y+F=0";
V1(COLOR):=RGB(cr(I),cg(I),cb(I));
CHECK(1);
// Plot View
STARTVIEW(1,1);
END;

Below are some examples. Remember the form:

Ax^2 + By^2 + Cxy + Dx + Ey + F = 0

Projectile Motion for HP Prime

This program calculates range and height of a projectile, and plots its path. The program sets the mode into Degrees (HAngle=1) and the calculator to the Parametric app.

Equations:
x = V * cos θ * t
y = V * sin θ * t - .5 * g * t^2

Where
V = initial velocity
θ = initial degree of flight
g = Earth gravitation constant (9.80665 m/s^2, ≈32.17404 ft/s^2)

Air resistance is not factored, so we are dealing with ideal conditions. How much the projectile represents reality varies, where factors include the object being projected, the temperate and pressure of the air, and the weather.

EXPORT PROJ13()
BEGIN
LOCAL M, str;
// V, G, θ are global
// Degrees
HAngle:=1;

CHOOSE(M, "Units", "SI", "US");
IF M==1 THEN
str:="m";
G:=9.80665;
ELSE
str:="ft";
G:=32.17404;
END;

INPUT({V, θ}, "Data",
{"V:","θ:"},
{"Initial Velocity in "+str+"/s",
"Initial Angle in Degrees"});

X1:="V*COS(θ)*T";
Y1:="V*SIN(θ)*T-.5*G*T^2";

STARTAPP("Parametric");
CHECK(1);
// Adjust Window
Xmin:=0
// Range
Xmax:=V^2/G*SIN(2*θ);
Ymin:=0
// Height
Ymax:=(V^2*SIN(θ)^2)/(2*G);
MSGBOX("Range: "+Xmax+" "+str+", "
+", Height: "+Ymax+" "+str);
// Plot View
STARTVIEW(1,1);
END;

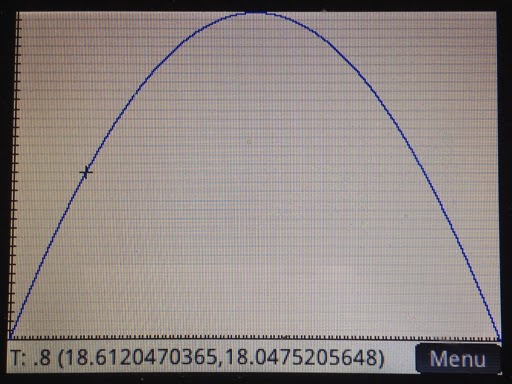
Below are screen shots from an example with V = 35.25 m/s and θ = 48.7°.

This concludes this session of the tutorials. Shortly I will have Part 6 up, which has to do routines.

I am catch-up mode, still. But then again I always feel like there is too much to do and too little time. LOL

See you soon!

Eddie


This blog is property of Edward Shore. 2013

HP Prime Programming Tutorial #4: CHOOSE and CASE, Tip about INPUT

Welcome to Part 4 of our programming series for the Prime. Today's session will cover CHOOSE and CASE.

---

First a tip from Han of the MoHPC Forum, which is found at http://www.hpmuseum.org/cgi-sys/cgiwrap/hpmuseum/forum.cgi#255084. Thank you Han for allowing me to share this.

Use the IF THEN ELSE structure with INPUT to execute a set of default instructions if the user presses cancel. INPUT returns a value of 0 if ESC or cancel is pressed, and 1 if a value is entered.

IF INPUT(...) THEN
commands if values are entered
ELSE
commands if Cancel is pressed
END;

Default values can be assigned to values as an optional fifth argument for INPUT.

INPUT(var, "Title", "Prompt", "Help", default value)

The type of variable maybe set to other than real numbers. Just remember to store such type before the INPUT command. For example, if you want var to be a string, store an empty string:

var:=" ";

Again, major thanks to Han.

---

CHOOSE and CASE

CHOOSE: Creates a pop up choose box, similar to what you see when you click on a soft menu. There are two syntaxes for CHOOSE:

Simple Syntax (up to 14 options):
CHOOSE(var, "title string", "item 1", "item 2", ... , "item n");

List syntax (infinite amount of items):
CHOOSE(var, "title string", {"item 1", "item 2"});

Choosing item 1 assigns the value of 1 to var, choosing item 2 assigns the value of 2 to var.

Access: Cmds, 6. I/O, 1. CHOOSE

---

CASE: Allows for different test cases for one variable. Also includes a default scenario (optional).

CASE
IF test 1 THEN do if true END;
IF test 2 THEN do if true END;
...
DEFAULT commands END;

Access: Cmds, 2. Branch, 3. CASE

Let's look at two programs to demonstrate both CHOOSE and CASE.

---

TERMVEL - Terminal Velocity of an Object

EXPORT TERMVEL()
BEGIN

LOCAL L0:={9.80665,32.174},
L1:={1.225,.0765},
L2:={.47,1.05,1.15,.04},C,K,M,A,T;

CHOOSE(C,"Units","SI","English");

CHOOSE(K,"Type of Object","Sphere","Cube",
"Cylinder","Tear-Shaped");

INPUT({M,A},"Object",
{"M=","A="},{"Mass","Surface Area"});

T:=√((2*M*L0(C))/(L1(C)*A*L2(K)));

MSGBOX("Terminal Velocity="+T);
RETURN T;
END;

---

Examples:

Sphere, SI Units, M = .05 kg, A = .0028 m^2
Terminal Velocity: T = 24.6640475387 m/s

Cube, US Units, M = 1.2 lb, A = .3403 ft^2
Terminal Velocity: T = 53.149821209 ft/s

---

AREAC - Area of Circles, Rings, and Sectors

EXPORT AREAC()
BEGIN
LOCAL C,R,S,θ,A;
CHOOSE(C,"Areas","1. Circle","2. Ring","3. Sector");

INPUT(R, "Input Radius", "R =");

CASE
IF C==1 THEN A:=π*R^2; END;

IF C==2 THEN
INPUT(S,"Small Radius","r=");
A:=π*(R^2-S^2);
END;

IF C==3
INPUT(θ, "Angle", "θ=");
\\ Assume you are in the correct angle mode
IF HAngle==1 THEN
\\ Test Angle Mode
θ:=θ*π/180;
END;
A:=θ*R^2/2;
END;

END;

MSGBOX("Area is "+A);
RETURN A;
END;

---

Examples

R = 2.5, r = 1.5, θ = π/4 radians or 45°

Circle: 19.6349540849
Ring: 12.5663706144
Sector: 2.45436926062

---

That is how, in general CHOOSE and CASE work. I thank you as always. It is so good to finally be rid of a cold and firing on all cylinders again.


Eddie

This blog is property of Edward Shore. 2013

HP Prime Programming Tutorial #3: WHILE, INPUT, KILL, REPEAT, GETKEY

This tutorial is going to cover a lot, each with some new programming commands in this series. I hope you are ready for the intensity. :)

---

WHILE, INPUT, KILL

HP Prime Program: TARGET. TARGET is a game where you provide a guess to get a desired number. If you miss, the calculator will tell you if number is higher and lower. At the end of the game, the calculator gives you how may picks you needed to get the target number.

WHILE: Repeat a number of commands while a specific condition is test.

WHILE condition is true DO
commands
END;

Access: Tmplt, 3. Loop, 5. WHILE

Caution: Watch your ENDs! Make sure an END is with each loop and the program itself. Press the soft key Check to check your work.

INPUT: Creates an input screen for variables. On the HP Prime, the input can asked for more than one input. TARGET demonstrates INPUT with one prompt.

One Variable:
INPUT(variable, "title", "label", "help text")
Multi-Variable:
INPUT(list of variables, "title", list of "labels", list of "help text")

Note: Pressing Cancel will store a 0 in variable. You may include code of what to do if the user presses Cancel, but it is not required.

Access: Cmds, 6. I/O, 5. INPUT

KILL: Terminates program execution. Nothing dies, I promise.

Access: Tmplt. 1. Block, 3. KILL

---

Program:
EXPORT TARGET()
BEGIN
LOCAL C:=0, N:=RANDINT(1,20), G:=-1;
WHILE G≠N DO
C:=C+1;
INPUT(G,"Guess?","GUESS:","1 - 20");

IF G==0 THEN
KILL;
END;

IF G < N THEN
MSGBOX("Higher");
END;

IF G > N THEN
MSGBOX("Lower");
END;

END;

MSGBOX("Correct! Score: "+C);

END;

---

Try it and of course, you can adjust the higher limit. Here is some thing for you to try with TARGET:

1. Add a limited amount of guesses.
2. Can you display the list of guesses?

---

REPEAT

ULAM Algorithm: take an integer n. If n is even, divide it by 2. If n is odd, multiply it by 3 and add 1. ULAM counts how many steps it takes to get n to 1.

REPEAT:

Access: Tmplt, 3. Loop, 6. REPEAT

Featured:
CONCAT(list1, list2): Melds list1 and list2 into one.

Access: Toolbox, Math, 6. List, 4. Concatenate

---

EXPORT ULAM(N)
BEGIN
LOCAL C:=1, L0:={N};

REPEAT

IF FP(N/2)==0 THEN
N:=N/2;
ELSE
N:=3*N+1;
END;

C:=C+1;
L0:=CONCAT(L0,{N});
UNTIL N==1;

MSGBOX("NO. OF STEPS="+C);
RETURN L0;
END;

---

Examples:

ULAM(5) returns:
Message Box: "NO. OF STEPS=6"
List: {5, 16, 8, 4, 2, 1}

ULAM(22) returns:
Message Box: "NO. OF STEPS=16"
List: {22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1}

---

GETKEY

The next section will introduce a super-important command, GETKEY. We will be working with GETKEY over the entire series.

The Program KEYNO: The person presses key presses. Which each key press, the code returns to the terminal screen. The program terminates when the Enter key is pressed.

GETKEY: Returns the key code of last key pressed. The Prime's key map is below. (Picture is from the HP Prime User's Guide)

Access: Cmds, 6. I/O, 4. GETKEY

EXPORT KEYNO()
BEGIN
LOCAL K;
PRINT();
PRINT("Press any key to get its code.");
PRINT("Press Enter to exit.");

REPEAT
K:=GETKEY;
IF K ≥ 0 THEN
PRINT(K);
END;
UNTIL K==30;

END;

---

Example Key Codes:
33: 8 key
2: up
7: left
8: right
12: down
50: plus
45: minus

---

This concludes Part 3. Again, it can't be said enough, thanks for all the comments and compliments. And until next time,

Eddie


This blog is property of Edward Shore. 2013

HP Prime Tip: RPN and Created Programs

Major thanks to Miguel Toro from the MoHPC Forum for this tip:

There are two ways to call created programs in RPN mode of the HP Prime:

Vertically:
argument 1 [Enter]
argument 2 [Enter]
...
argument n [Enter]
program [Enter]

Horizontally:
argument 1 [space] argument 2 [space] ... argument n [space] program
[Enter]

Keep in mind this works with created user programs. To ensure that built-in commands work correctly, still include the number of arguments as needed.

Link to the forum: http://www.hpmuseum.org/cgi-sys/cgiwrap/hpmuseum/forum.cgi


Eddie


This blog is property of Edward Shore. 2013

Matrix Calculations: det(A - B * λ)=0

Let A and B be square matrices. B is a diagonal matrix. A diagonal matrix is a matrix with entries in it's diagonal positions, (1,1), (2,2), and so on, and 0 everywhere else. The identity matrix is a diagonal matrix. Another example is:

[ [2, 0, 0],[0, -2, 0],[0, 0, 5] ]

Let m, n, r, s, and t be numerical constants. Let a1, a2, and a3 be entries on the first row. Similar for b1, b2, b3, c1, c2, and c3.

det(A - B * ident(λ)) = 0

---

Comparison of 2 x 2 Matrices:
Note the constant term (λ^0), typed in green, the same.

B is a 2 x 2 identity matrix.

det( [ [a1, a2],[b1, b2] ] - λ * [ [1,0],[0,1] ] ) = 0
det( [ [a1, a2],[b1, b2] ] - [ [λ, 0],[0, λ] ]) = 0
λ^2 - (a1 + b2) * λ + a1*b2 - a2*b1 = 0

B is a diagonal matrix [ [m, 0],[0, n] ].

det( [ [a1, a2],[b1, b2] ] - λ * [ [m,0],[0,n] ] ) = 0
det( [ [a1, a2],[b1, b2] ] - [ [m*λ, 0],[0, n*λ] ]) = 0
m*n*λ^2 - (a1*n + b2*m)*λ + (a1*b2 - a2*b1) = 0

---

Comparison of 3 x 3 Matrices:
Note the constant term (λ^0), typed in green, the same.

B is a 3 x 3 identity matrix.

det( [ [a1,a2,a3],[b1,b2,b3],[c1,c2,c3] ] - λ * [ [1, 0, 0],[0, 1, 0],[0, 0, 1] ] ) = 0
det( [ [a1,a2,a3],[b1,b2,b3],[c1,c2,c3] ] - [ [λ, 0, 0],[0, λ, 0],[0, 0, λ] ] ) = 0

- λ^3
+ λ^2 * (a1 + b2 + c3)
+ λ * (-a1*b2 - a1*c3 - b2*c3 + a2*b1 + a3*c1 + b3*c2)
+ (a1*b2*c3 - a1*b3*c2 - a3*b2*c1 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2) = 0

B is a general 3 x 3 diagonal matrix, [ [r, 0, 0],[0, s, 0],[0, 0, t] ].

det( [ [a1,a2,a3],[b1,b2,b3],[c1,c2,c3] ] - λ * [ [r, 0, 0],[0, s, 0],[0, 0, t] ] ) = 0
det( [ [a1,a2,a3],[b1,b2,b3],[c1,c2,c3] ] - [ [r*λ, 0, 0],[0, s*λ, 0],[0, 0, t*λ] ] ) = 0

- λ^3 * r*s*t
+ λ^2 * (s*t*a1 + r*t*b2 + r*s*c 3)
+ λ * (a1*b2*c3 - a1*b3*c2 - a3*b2*c1 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2) = 0


Of course to get the eigenvalues (λ), solve the appropriate polynomial.

Hope this is helpful to those studying linear algebra or for those who are curious. This post was inspired from a program I was helping a fellow HP Prime programmer.

This post is dedicated to Michael de Estrada.


This blog is property of Edward Shore. 2013

HP Prime Programming Tutorial #2: MSGBOX, IF-THEN-ELSE, PRINT, FOR

Welcome to another programming tutorial for the HP Prime. In this session, we will cover MSGBOX, IF-THEN-ELSE, PRINT, and the FOR loop.

---

MSGBOX

MSGBOX: MSGOX takes a string a makes a pop-up message box. Program execution stops until you press a key to acknowledge the message.
Access: Cmds, 6. I/O, 8. MSGBOX

The program COMLOCK: Imagine that you are in charge of setting the combinations for the good, old-school combination locks. This program gives three digit combinations through the use of MSGBOX.

EXPORT COMLOCK()
BEGIN
LOCAL L0;
L0:=RANDINT(3,0,39);**
MSGBOX("SECRET: "+L0(1)+","+L0(2)+","+L0(3));
END;  
** Thanks to Thomas Lake for pointing out my typo.  Apologies for any inconvenience - Eddie (3/21/2014)

---

Other commands that are featured:

RANDINT(n, a, b) generates a list of n integers between a and b. You can leave n out if you desire a single random integer. Picks may be repeated.

The HP Prime's default list variables are designated L0 through L9.

---

Here is a sample output for COMLOCK:

IF-THEN-ELSE

IF-THEN-ELSE: Program structure:
IF condition THEN
do if the condition is true;
ELSE
do if the condition is false;
END;

Access: Tmplt, 2. Branch, 2. IF THEN ELSE

---

Tip: You can leave out the ELSE part if you only want to test to see if a condition is true. Access the simple IF-THEN structure by pressing Tmplt, 2. Branch, 1. IF THEN.

Access <, ≤, ==, etc. by pressing Shift, 6. Note that the double equals is needed to check equality.

---

PRINT

PRINT: The PRINT command prints a sting, result, or a combination of both onto the Prime's Terminal screen. If PRINT is used, the program will end on the terminal (text output) screen. Press a button to exit.

You can access the terminal screen at any time by pressing the ON button, holding it, and then pressing the Divide ( ÷ ) button.

Access: Cmds, 6. I/O, 9. PRINT

---

Tip: To clear the terminal screen, type PRINT(). This is a good way to clear the terminal screen and I usually use this at the beginning of any program if PRINT is going to be used later on.

---

The program QROOTS (yet one more quadratic solver, sorry for not being original guys and gals), demonstrates the use of IF-THEN-ELSE and PRINT.

Here I set the setting variable HComplex to 1, which allows for complex number results.

EXPORT QROOTS(A,B,C)
BEGIN
LOCAL D;
PRINT();
HComplex:=1;
D:=B^2-4*A*C;
IF D≥0 THEN
PRINT("Roots are real.");
ELSE
PRINT("Roots are complex.");
END;
PRINT((-B+√D)/(2*A));
PRINT((-B-√D)/(2*A));
END;

Examples:

QROOTS(1,5,8) returns:

Roots are complex.
-2.5+1.32287565553*i
-2.5-1.32287565553*i

QROOTS(2,-4,-8) returns:

Roots are real.
3.2360679775
-1.2360679775

---

FOR

This section will explore the basic FOR structure:

FOR variable FROM start TO end DO
commands;
END;

All the commands in the loop will be executed a set number of times. Each time a loop finishes, the variable increases by one. The loop terminates when variable=end.

Access: Tmplt, 3. LOOP, 1. FOR

---

The program SUMDIV takes any integer and adds up the sum of its divisors. For example, the divisors of 12 are 1, 12, 2, 3, 4, and 6. The sum is 28.

---

Featured Commands in SUMDIV:

idivis: idivis(integer) returns a sequence of all of the divisors if integer. Access: Toolbox, CAS, 5. Integer, 1. Divisors

Any CAS command used in programming will be preceded by "CAS." Not all CAS commands can be used in HP Prime programming at this time.

DIM: returns the dimensions of a sequence, string, or matrix. DIM must be used instead of SIZE to prevent a Bad Argument error.

For sequences or vectors, DIM returns the length in a list {length}.
For strings, DIM returns length as a number.
For matrices, DIM returns the list {number of rows, number of columns}.

Access: Cmds, 1. Strings, 9. DIM

---

The program:

EXPORT SUMDIV(N)
BEGIN
LOCAL S:=0,K,mdiv,ldiv;
mdiv:=CAS.idivis(N);
ldiv:=DIM(mdiv);
FOR K FROM 1 TO ldiv(1) DO
S:=S+mdiv(K);
END;
RETURN S;
END;  

** Thanks to Thomas Lake for pointing out that the variable "mat", which I had in this program was unnecessary.  - Eddie 3/21/2013

 

Examples:
SUMDIV(12) returns 28.
SUMDIV(24) returns 60.
SUMDIV(85) returns 108.

---

This concludes this part of the HP Prime Programming Tutorial.

HAPPY HALLOWEEN!

Eddie


This blog is property of Edward Shore. 2013

HP Prime Programming Tutorial #1: LOCAL, RETURN

Over the next month, maybe month and a half, I plan to post programming tutorials for the HP (Hewlett Packard) Prime.

If you have programmed with the HP 38G, 39g, or 39gii, this language will be similar to those. The programming language for the Prime is named the HP Prime Programming Language (HPPP).

Throughout this tutorial, I am going to use the latest version of the software.

How to start writing a program:

1. Press Shift + 1 (Program).
2. Press New. It is the second touch key.
3. Enter the name of the program. Pressing the ALPHA key twice will turn on UPPERCASE ΑLPHA-LOCK. Pressing ALPHA, Shift, ALPHA will turn on lowercase alpha-lock. To exit any lock, press the ALPHA key one more time. When happy with the name, press Enter.

---

Rules for Program Names:

1. Letters, numbers, and the underscore character (_) only.

2. The program name must start with a letter.

---

Structure of a HP Prime Program

A HPPP program is encased of an EXPORT - BEGIN - END structure. The layout is generally like this:

EXPORT program_name(arguments)
BEGIN
commands and comments go here
END;

Each line containing a command generally must end with a semicolon (;). A semicolon can by type by pressing ALPHA then the Plus key ( + ).

Comments can be typed. The are designated by two forward slashes. The slashes are typed by pressing the Divide key ( ÷ ). Anything in the line following the two slashes is ignored in running the program.

---

SQIN

Our first program is SQIN, because "Hello World" programs are so 2000s. SQIN takes a number, squares it, then calculates the reciprocal. In short we are defining a custom function:

SQIN(x) = 1/x^2

Commands:

RETURN: returns a result to the stack (home page). You can return numbers, lists, vectors, matrices, strings, or a combination of these times.
Access: Tmplt, 1. Block, 2. RETURN

All the program code in this tutorial series will be shown in Courier font.

EXPORT SQIN(X)
BEGIN
RETURN 1/X^2;
END;

---

Tip: You can check the syntax of the program just by pressing the Check soft key in the program editor. HP Prime will inform you if there is a syntax error and attempt to point you to the error. If there are no syntax errors, the Prime states "No errors in the program". I use the Check command all the time.

---

How to run the programs:

Home Mode - Textbook Entry,
Home Mode - Algebraic Entry,
CAS Mode:

Type the program name. Follow the name with parenthesis and enclose the required arguments.

Or use the Toolbox (top row of white keys, 2nd key from the left, it looks like a tool box), select the User touch key, select the program, and input the required arguments.

Home Mode - RPN Entry:

Enter each argument, separate each entry by pressing the Enter key. Type the name, and in the parenthesis state the number of arguments.

For example, if the program TEST has four arguments, the RPN stack would like this:

4: argument_1
3: argument_2
2: argument_3
1: argument_4
TEST(4) to run the program.

---

Examples to try with SQIN:

SQIN(5) returns .04
SQIN(36) returns .000771604938


The next program will demonstrate the concept of local variables.

---

MOPMT

LOCAL: Declares any variables to be local to the program. In other words, the variables are created, used, possibly displayed during program execution, and deleted at program termination.
Access: Tmplt, 4. Variable, 1. LOCAL

---

Tip: You can declare local variables and assign an initial value at the same time. For example: LOCAL K:=1; stores 1 in K and makes K a local variable.

---

MOPMT calculates the monthly payment of a loan. The arguments are: the loan amount (L), the interest rate (R), and the number of months (M).

EXPORT MOPMT(L,R,M)
BEGIN
LOCAL K:=R/1200;
K:=L*K/(1-(1+K)^-M);
RETURN "Payment ="+K;
END;

---

Tip: Use RETURN, TEXTOUT_P, and PRINT to return custom strings, which combine results, messages, and calculations. Parts are connected with a plus sign.

---

Examples:
MOPMT(4000, 9.5, 30) returns 150.317437565
MOPMT(370000, 3.5, 360) returns 1661.46534383

Try this and next time in the series I will highlight other things we can do with HPPP. Thanks!

Eddie

This blog is property of Edward Shore. 2013 

Program: Operations with Large Numbers (HP Prime)

Operations with Large Numbers

Large Factorial (Version 2) - HP Prime

EXPORT LFACT(N)
BEGIN
LOCAL K,S,A;
FOR K FROM 2 TO N DO
S:=S+LOG(K);
END;
RETURN { ALOG(FP(S)), IP(S) };
END;

This is an approximation! Results: {mantissa, exponent}. To be interpreted like this: mantissa * 10^exponent

Examples (compared with actual calculations with HP 50g):

55!
LFACT: 1.2696403353 * 10^73
Actual: 1.26964033537 * 10^73

65!
LFACT: 8.24765059247 * 10^90
Actual: 8.24765059208 * 10^90

75!
LFACT: 2.48091408072 * 10^109
Actual: 2.48091408114 * 10^109

125!
LFACT: 1.88267716466 * 10^209
Actual: 1.88267717689 * 10^209

245!
LFACT: 3.44638099725 * 10^480
Actual: 3.44638108855 * 10^480

525!
LFACT: 6.89080261728 * 10^1201
Actual: 6.89080262404 * 10^1201

875!
LFACT: 1.31677044437 * 10^2196
Actual: 1.31677038751 * 10^2196

Large Powers - HP Prime

EXPORT LPWR(X,Y)
BEGIN
LOCAL S;
S:=Y*LOG(X);
RETURN { ALOG(FP(S)), IP(S) };
END;

This is an approximation! Results: {mantissa, exponent}. To be interpreted like this: mantissa * 10^exponent

Examples (compared with actual calculations with HP 50g):
50^38
LPWR: 3.63797880819 * 10^64
Actual: 3.63797880709 * 10^64

102^68:
LPWR: 3.84425050422 * 10^136
Actual: 3.84425050254 * 10^136

58^124:
LPWR: 4.624568333 * 10^218
Actual: 4.62456834156 * 10^218

302^219:
LPWR: 1.32288017481 * 10^543
Actual: 1.32288017363 * 10^543




This blog is property of Edward Shore. 2013

Calculus Lesson: Area Between Curves

Area Between Two Curves

The general formula for finding the area between two curves is:

b
∫ T(x) - B(x) dx
a

I named the functions T(x) and B(x) specifically. T(x) represents the function "on top", while B(x) represents the function "on the bottom". In short, for x ∈ (a,b), T(x) ≥ B(x).

Here is an approach to use when finding areas between curves. A graphing calculator or mathematical software can be helpful in this procedure.

1. Draw the graphs. This is where a graphing calculator comes in handy.

2. Determine a and b, your limit points. Sometimes one or both of the limit points are found by finding the intersection of the two curves. Other problems will give you a third (or even fourth) condition. An example is x≥0, which makes one of our limit points x=0.

3. Determine which of the curves is T(x) and B(x). T(x) has greater numerical value than B(x) over the interval x ∈ (a, b).

4. Take the definite integral of T(x) - B(x). The result is your area.

b
∫ T(x) - B(x) dx = Area
a


About the examples and problem set: Please note that most examples in math textbooks, the numbers come out "nice and neat". Not so here, so I am using an HP Prime to demonstrate these examples and come up with answers. (any graphing calculator, HP, TI, Casio, all will do just fine!)

Example 1:

Find the area between:
y = -x^2 + 2
y = x^2 + 1

Here is a graph of the two curves:

Finding the limit points:

-x^2 + 2 = x^2 + 1
1 = 2*x^2
1/2 = x^2
Which implies x = -1/√2 and x = 1/√2

So our limit points are a = -1/√2 and b = 1/√2

From the graph we note that:
T(x) = -x^2 + 2
B(x) = x^2 + 1
and
T(x) - B(x) = -x^2 + 2 - (x^2 + 1) = -2*x^2 + 1

Taking the integral:

1/√2
∫ -2*x^2 + 1 dx ≈ 0.94281
-1/√2

So the area for Example 1 is about 0.94281.

Example 2:

Find the area between the two curves:
y = 2 cos x
y = x - 2
With the condition x≥0

First we graph the two curves:

The two graphs intersect when x>0. Since we are given the additional condition that x≥0, the lower limit for this problem is a=0.

To find the upper limit, we find intersection point:
2 cos x = x - 2
2 cos x - x + 2 = 0

Using a numeric solver on a calculator, we find that the intersection point is x ≈ 1.71419. (See, the numbers in these examples aren't always as "neat").

In the region x ∈ (0, 1.71419), we see that 2 cos x > x - 2. Hence:

T(x) = 2 cos x
B(x) = x - 2
and the area is approximately

1.71419
∫ 2 cos x - (x + 2) dx ≈ 3.93863
0

Problems to Try

Problem 1
Find the area between the curves of
y = x^2
y = 4

Problem 2

y = x^3
y = -3*x + 8
With the condition x≥0

Problem 3

y = 8*x^2 + 4*x - 6
y = x

Check your answers:
Areas are rounded to five decimal points:
1. 10.66667
2. 7.36017 (Hint: Upper Limit ≈ 1.51275)
3. 7.42101 (Hint: Use a calculator to find the limit points)


Any questions, please leave them in the comment box. Hope this is helpful and thanks!


Eddie


This blog is property of Edward Shore. 2013

HP 35S: Resistors in Series or Parallel (Portred from HP-33E)

Resistors in Series or Parallel
Source: HP-33E Student Engineering Applications, 1978
Original Calculator: HP-33S
Credit to Hewlett Packard Company
Ported to HP 35S by Eddie Shore, 10/10/2013

Instructions:
1. For each group of parallel or series resistors: press XEQ R.
2. At the Mode Prompt (INPUT M), enter 0 R/S for Parallel Resistors, 1 R/S for Series Resistors
3. Enter resistor values (assumed to be in Ohms) then press R/S.
4. To find the total, press XEQ R016.
5. Optional: Store the result in a variable for future use, as long is it not R.

Parallel Resistors: total resistance = 1/( 1/R1 + 1/R2 + ... )

Series Resistors: total resistance = R1 + R2 + ...


Program:
R001 LBL R
R002 0
R003 STO R
R004 SF 10 // press Left Shift, Flags, SF, decimal point, 0
R005 0=PAR 1=SER // equation
R006 PSE
R007 CF 10 // press Left Shift, Flags, CF, decimal point, 0
R008 INPUT M
R009 R/S
R010 RCL M
R011 x=0?
R012 XEQ R024
R013 R-down
R014 STO+ R
R015 GTO R009

R016 RCL R // total resistance
R017 RCL M
R018 x=0?
R019 XEQ R024
R020 CLx
R021 STO M
R022 R-down
R023 RTN

R024 R-down
R025 1/x
R026 ENTER
R027 RTN

Example 1:

Keystrokes:
1st Set:
XEQ R ENTER
0 R/S
120 R/S
240 R/S
120 R/S
XEQ R016
STO T

2nd Set:
XEQ R ENTER
0 R/S
320 R/S
400 R/S
XEQ R016
STO U
RCL+ T

Total Resistance: 225 7/9 ohms

Example 2:

XEQ R ENTER
0 R/S
30 R/S
60 R/S
XEQ R016 // Result: 20
STO T

XEQ R ENTER
1 R/S
RCL T R/S
80 R/S
XEQ R016 // Result: 100
STO T

XEQ R ENTER
0 R/S
RCL T R/S
40 R/S
XEQ R016

Total Resistance: 28 4/7 ohms

Interesting Base Conversions - Porting a 1975 HP 25 Program to the HP 35S

Sometimes simple is best.

Base N to Base 10
Source: HP 25 Applications, 1975, pg. 22
Credit to Hewlett Packard Company
10/8/2013

Instructions:
Store the base of the number to be converted in B.
Start with the left most integer, press XEQ B. For each successive integer, press R/S. This is the integer portion.
Start with the left most fractional part, press XEQ B016. For each successive fractional digit, press R/S.

Examples:
1777 base 8 → 1023
143.2044 base 5 → 48.4384
1.11011 base 2 → 1.84375
B3A.F base 16 → 3131.9375

Program:
B001 LBL B
B002 STO A
B003 RCL B
B004 ENTER
B005 ENTER
B006 ENTER
B007 RCL A
B008 R/S
B009 STO A
B010 CLx
B011 +
B012 x
B013 RCL A
B014 +
B015 GTO B008
B016 RCL B
B017 1/x
B018 STO C
B019 STO D
B020 x
B021 R/S
B022 RCL C
B023 RCL D
B024 x
B025 STO D
B026 x
B027 +
B028 GTO B021

Base 10 to Base N
Source: HP 25 Applications, 1975, pg. 24
Credit to Hewlett Packard Company
10/8/2013

Instructions:
1. Store the number to be converted in A
2. Store the desired base in B
3. Press R/S stop. The approximation will build and keep building indefinitely until stopped.

Examples:
67.32 → 4 03. 05 01 14 11 base 16 (≈43.51EA base 16)
π ≈ 11.001001 base 2

√2 ≈ 1.0110101 base 2

Program:
T001 LBL T
T002 RCL B
T003 10
T004 x≥y?
T005 GTO T007
T006 100
T007 STO C
T008 0
T009 STO D
T010 RCL A
T011 LN
T012 RCL B
T013 LN
T014 ÷
T015 x<0?
T016 GTO T019
T017 IP
T018 GTO T022
T019 IP
T020 1
T021 -
T022 STO E
T023 RCL C
T024 x<>y
T025 y^x
T026 RCL D
T027+
T028 STO D
T029 PSE
T030 RCL B
T031 RCL E
T032 y^x
T033 STO - A
T034 GTO T010


This blog is property of Edward Shore. 2013

Jeppesen E68 Wind Easy Computer

This past Sunday at the Pasadena City College Swap Meet, I found and bought a Jeppensen E6B Wind-Easy Computer. In reality, the E6B-2A is a slide rule specialized for aviation. The box may have not been in the best shape, how every he slide rule, its metal insert, instruction manual, and carrying pouch are all in great condition.

The E6B-2A has two sides: a calculator side and a wind side.

Though my schedule has not allowed me much time to work with the E6B-2A, from the manual each of the two sides of the slide rule allows for specific calculations.

Calculator Side:
* Computation of speed, distance, and time
* Distance conversions: kilometers, miles, and nautical miles, which each of the measuring guides marked on the outside scale.
* Altitude Calculations: Density and True Altitude
* True Air Speed
* Mach Speed
* Slide rule, where the outer and inner scales act as scales C and D, respectively.

Wind Side:
* Calculations involving the "wind triangle", made up of the wind vector, ground vector, and air vector.
* Using the wind charts to plot true speed and course.

I have never owned a slide rule like this before, very interesting and unique - and something to carve out some time to learn. Very cool item!

Eddie


This blog is property of Edward Shore. 2013

.

HP Prime Program: Sampling Without Replacement

SAMPLE - Generate a list of random integers from 1 to N using sample without replacement.

Author: Eddie Shore
Date: 10/1/2013

Syntax: SAMPLE(L, N)
L = length of desired list
N = high integer
If L > N, an error occurs.

Output: random sample

Program:
EXPORT SAMPLE(L,N)
BEGIN
// length, number
LOCAL I, K, T, num;

// error cond
IF L > N THEN
1/0;
END;

// main program
L1:=MAKELIST(0,X,1,L,1);
L1(1):=RANDINT(N-1)+1;
I:= 2;

REPEAT
num:=RANDINT(N-1)+1;
T:=1;

// test for uniqueness
FOR K FROM 1 TO I DO
IF num == L1(K) THEN
T:=T + 1;
END;
END;

IF T == 1 THEN
L1(I) := num;
I := I + 1;
END;

UNTIL I == L + 1;
RETURN L1;
END;

Examples:
SAMPLE(5,9) (length of 5, n = 9) can generate:
{5, 4, 8, 2, 6}
{9, 7, 8, 1, 2}
{4, 3, 6, 5, 2}


This blog is property of Edward Shore. 2013

HP Prime Program: ULAM

ULAM - Using Ulam's Conjecture to determine the number of steps it takes to reduce an integer N to 1 using the following rules:

If N is odd: N = 3×N+1
If N is even: N=N/2

9/24/2013

Program:

EXPORT ULAM(N)
BEGIN
LOCAL C;
PRINT();
REPEAT
IF FP(N/2)==0 THEN
N:=N/2;
ELSE
N:=3*N+1;
END;
C:=C+1;
PRINT(N);
UNTIL N==1;
RETURN C;
END;

Examples:
ULAM(69): 208, 104, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 (14 steps)

ULAM(84): 42, 21, 64, 32, 16, 8, 4, 2, 1 (9 steps)


This blog is property of Edward Shore. 2013

HP Prime Tip: Changing the Color of a Function

In the graphing apps of the HP Prime, like the Function, Advanced Graphing, Parametric, and Polar apps, expressions can be graphed in various colors.

There are two ways to change the colors of a graph. First, the easy, but limited way.

For this example, I am going to use the Function App with F1(X) = 2 * e^(SIN(X)). Assume the View is set to Autoscale.


1. Press the Symb key. To the left of the expression box is the color box. Move left until the color box is highlighted. You will know that the color box is highlighted when the screen says "Choose graph color".

2. Hit the Choose soft key. An array of nine colors will appear. Choose the desired color and press Enter. For this example I will select red.

Here is F1 graphed in red:

However, what if you want to:
1. Graph the function in a color other than the nine presented in the Symbolic page? (This includes black)
2. Be able to change the color of the function in a program?

We can do that too, with the following:

F1(COLOR):=#RRGGBBh where RRGGBBH is a hexadecimal code, or
F1(COLOR):=RGB(red, green, blue)

You can type the command in either Home mode set to Textbook or Algebraic Entry or Program Editor mode.

---

Caution: Doing this in CAS mode will result in the color code stored in the function - not desirable.

---

If you are in Home Mode, RPN Entry, either:

1. Enter the hexadecimal code
2. Press Enter
3. Type 'F#(COLOR)' in single quotes. Press Enter. (use the appropriate name and type).
4. Press Shift+EEX (STO>).

or

1. Enter the red intensity, press Enter
2. Enter the green intensity, press Enter
3. Enter the blue intensity, press Enter
4. Execute RGB(3). In RPN mode, the 3 tells the Prime to take the last three stacks as the arguments of RGB.
5. Type 'F#(COLOR)' in single quotes. Press Enter. (use the appropriate name and type)
6. Press Shift+EEX (STO>).

---

The maximum values for each of the colors is 255, or FF in base 16. This is similar to the range of colors you can choose from on a typical personal computer program. 0 is the least intense, 255 is the most intense.

For a list of colors and their color codes, one of the web pages you can visit is http://www.rapidtables.com/web/color/Web_Color.htm. Scroll down to see a table that has both hexadecimal and RGB codes.

Let's demonstrate with F1(X) = 2 * e^(SIN(X)).

First graph F1 in black. The RGB code for black is RGB(0,0,0) or #00000h. I have the calculator set to Home Mode, Textbook Entry.

Now plotting F1 in Dodger Blue, RGB(30,144,255) or #1E90FFh in Home Mode, RPN entry:

That is how to plot in color. Until next time,

Eddie


This blog is property of Edward Shore. 2013

HP Prime Tip: Setting Up User Keys

HP Prime User Keyboard Primer

On of the features of the new HP Prime is the ability to assign custom programs, mathematical commands, or constants to the keyboard.

In this tutorial, we will use the shortcut commands to set up a user keyboard. You can set one or many user keys, there is no required number. In addition, the user keyboard can take one of four planes:

Key
Shift + Key
ALPHA + Key
Shift + ALPHA + Key

We will illustrate the procedure by assigning the STRING() command to the
Change Sign [ +/- ] key.

1. Create a new program and give it any name you want. For this example, I name the program USERKEY. USERKEY is going to be where I store my user key assignments.

2. Clear the program editor. There should be no EXPORT-BEGIN-END structures on the screen.

3. Press the [Menu] key. The [Menu] key is on the upper right hand corner section of the keys, to the left of the [CAS] key and below the [View] key. Select option 4: "Create User Key".

4. At the "Press any key..." prompt, select the key for which you want to assign your command to.

For my illustration, I will press the [+/-] key.

5. The user key template will appear of the programming editing screen. In between the BEGIN and END; is where you will type.

Note that the appropriate key code will be entered for you.

6. Call the RETURN command by pressing the soft key (Tmplt) then selecting "Block" then "RETURN".

Type your command and program in quotes. You can also call them from the various HP Prime menus or the Catalog. It is very important that you end this line with a semicolon (;), otherwise a syntax error occurs.

Note that user key assignments and edits are saved automatically. There is no need to run the USERKEY program.

Illustrated below is me putting the STRING() command. This assigns the STRING command to the [ +/- ] key.

For additional key assignments, repeat steps 3-6. Each key assignment template stands alone. Do not nest key assignment templates.

To use a user-assigned key, first press [Shift] + [Help] (User). An orange "1U" indicator appears on the top left hand corner of the screen. This means the next key pressed will execute the user-assigned function (if there is one).

For my example, pressing [Shift] + [Help] (User), [+/-] brings up the STRING command.

That is all there is to it!

Be sure to take notes of your key assignments.

Look for additional HP Prime programming tutorials in the upcoming months.

As always thank you for your support and comments. Have a great day everyone,

Eddie


This blog is property of Edward Shore. 2013