Casio fx-5800P: Lambert Function by Pierre Gillet
The programs on this blog entry are created and authored by Pierre Gillet. Gratitude for his permission to post this on my blog.
Introduction
The Lambert function is defined as:
w = W(x) where w * e^w = x
W(x) is the inverse of y = x * e^x: so, W(x) * e^(W(x)) = x and W(x * e^x)=x
In all cases, x must be >= -1/e to get a real value of W(x)
For x>=0, there’s only one value of W(x), called W0(x) (« principal branch » of W(x))
For x<0, two values of W(x) are possible : W0(x) and W-1(x)
In all cases, W0(x) >= -1 and W-1(x) < = -1
The set of programs presented use W(x) to solve equations such as:
x^x = a
log x = x - 1
a^x = b - x
where a and b are real constants.
The trick to solve these kinds of equation is to transform them into the form
f(x) * e^f(x) = constant
Then comes
W(f(x) * e^f(x)) = W(constant)
f(x) = W(constant) (remember that W(x * e^x) = x)
and then you normally solve easily for x but still have to calculate the above W(constant)
You can calculate W(p) (where p is constant) with the efficient Newton’s method solving the equation x * e^x – p = 0:
To get W0(p) :
if -1/e <= p <= 10 then x_0 = 0
if p > 10 then x_0 = ln(p) – ln(ln(p)) (asymptotic behavior of W0(x))
To get W-1(p) :
If -1/e <= p <= -0.1 then x_0 = -2
if p > -0.1 then x_0 = ln(-p) – ln(-ln(-p)) (asymptotic behavior of W-1(x))
Then iterate x_n = (x^2 + p * e^(-x)) / (x + 1)
will normally converge to the desired W(p) value
See this post:
https://math.stackexchange.com/questions/463055/approximation-to-the-lambert-w-function
Programs :
"W0FX" // The program asks for x and displays W0(x) value (stored in W)
?X:0->G
X>10 => Ln(X)-Ln(Ln(X))->G
Prog "WSUB":W
"W-1FX" // The program asks for x and displays W-1(x) value (stored in W)
?X:-2->G
X>-.1 => Ln(-X)-Ln(-Ln(-X))->G
Prog "WSUB":W
"WSUB" // Subroutine called by W0FX and W-1FX
X<-e^(-1) => -1->G
10^(-10)->E:Lbl 1
(G^2+Xe^(-G))/(G+1)->W
Abs(G-W)<E => Return
W->G:Goto 1
Notes:
Precision is 1E-10 (see 10^(-10) in WSUB)
The first line in WSUB ensures Math error if X<-1/e
Note from Edward Shore:
?X is allowed on the fx-5800P: When executed, the last value of X is shown which can be accepted or replaced. It doesn't work for the Casio graphing calculators.
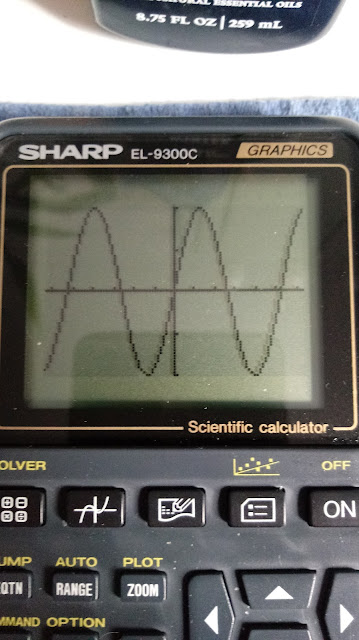
Below is a graph of x*e^x vs. W_0 from W0FX and W_-1 from W-1FX, as created by the Desmos graphing app:
Examples
x^x = 2
x * ln(x) = ln(2)
Let t = ln x (=>x = e^t)
t * e^t = ln(2)
W(t * e^t) = W(ln(2))
t = W(ln(2))
x= e^W(ln(2))
Ln(2) is >= 0 => Only one value for W: on W0(x)
Execute W0FX:
Type ln(2) then EXE
The program displays approx 0.4444 (ie W0(ln(2)))
You are out of the program and now type e^(W)
The machine displays approx 1.5596 (x value)
log x = x - 1
x = 10^(x - 1)
x = 10^x * 10^(-1)
x = e^(x * ln(10)) * 10^(-1)
x*e^(-x * ln(10)) = 10^(-1)
-x * ln(10) * e^(-x * ln(10)) = -10^(-1) * ln(10)
W(-x * ln(10) * e^(-x * ln(10))) = W(-10^(-1) * ln(10)
-x * ln(10) = W(-10^(-1) * ln(10)
x = -W(-10^(-1) * ln(10)) / ln(10)
-10^(-1) * ln(10))) is < 0 => Two values for W : on W0(x) and W-1(x)
Execute W0FX:
Type -10^(-1) * ln(10) then EXE
The program displays approx -0.3158 (ie W0(-10^(-1) * ln(10)))
You are out of the program and now type -W / ln(10)
The machine displays approx 0.1371 (first x value)
Then Execute W-1FX:
Press EXE (to keep the current value -10^(-1) * ln(10) in X) (approx -0.2303)
The program displays approx -2.3026 (ie W-1(-10^(-1) * ln(10)))
You are out of the program and now type -W / ln(10)
The machine displays approx 1 (second x value)
2^x = 11 - x
Let t = 11-x (=>x = 11-t)
2^(11 - t) = t
2^11 * 2^(-t) = t
2^11 * e^(-t * ln(2)) = t
e^(-t * ln(2)) = t / (2^11)
1 = t * e^(t * ln(2)) / (2^11)
ln(2) = t * ln(2) * e^(t * ln(2)) / (2^11)
2^11 * ln(2) = t * ln(2) * e^(t * ln(2))
W(2^11 * ln(2)) = W(t * ln(2) * e^(t * ln(2))
W(2^11 * ln(2)) = t * ln(2)
t = W(2^11 * ln(2)) / ln(2)
x= 11 - W(2^11 * ln(2)) / ln(2)
2^11 * ln(2) is >= 0 => Only one value for W: on W0(x)
Execute W0FX:
Type 2^11*ln(2) then EXE
The program displays approx 5.5452 (ie W0(2^11 * ln(2)))
You are out of the program and now type 11 – W / ln(2)
The machine displays approx 3 (x value)
What for numbers beyond 10^100 ?
Even for small values of the constants involved in an equation, you have to calculate W(x) with rapidly astronomical arguments :
For example, with the equation 2^x = 1000 – x (cf the 2^x = 11 – x case), you’d need to calculate W(2^1000 * ln(2)), causing overflow of most of the calculators.
Here again, you can calculate W(p) (where p is constant) with the efficient Newton’s method solving this time the equation ln(x) + x - ln(p) = 0, handling ln(p) instead of p:
To get W0(ln(p)):
x_0 = ln(p) – ln(ln(p)) (asymptotic behavior of W0(x))
Then iterate:
x_n = x * (1 - ln(x) + ln(p)) / (x + 1)
will normally converge to W0(p)
Additional programs
"W0FLNX" // The program asks for ln(x) and displays W0(x) value (stored in W)
?X:0->G
X-Ln(X)->G
Prog "WSUBLN":W
"WSUBLN" // Subroutine called by W0FLNX
10^(-10)->E:Lbl 1
G(1-Ln(G)+X)/(G+1)->W
Abs(G-W)<E => Return
W->G:Goto 1
Notes:
If p is an excessively large number then W0FLNX asks for ln(p) and returns W0(p). Enter ln(p) in a good way : for example, not ln(10^1000) but 1000 * ln(10)
2nd line in W0FLNX: "X - Ln(X)" is in fact ln(p) - ln(ln(p)) since you entered ln(p) in X
Example
2^x = 1000 - x
Solution : x = 1000 - W0(2^1000 * ln(2)) / ln(2)
(cf the Solve 2^x = 11 - x case)
2^1000 * ln(2) is >= 0 => Only one value for W: on W0(x)
2^1000 * ln(2) > 10^100 so you can’t execute W0FX
Note that ln (2^1000 * ln(2)) = 1000 * ln(2) + ln(ln(2))
Execute W0FLNX:
Type 1000 * ln(2) + ln(ln(2)) then EXE
The program displays approx 686.2494 (ie W0(2^1000 * ln(2)))
You are out of the program and now type 1000 - W / ln(2)
The machine displays approx 9.9514 (x value)
Thank you to Pierre Gillet.
Eddie
All original content copyright, © 2011-2022. Edward Shore. Programs provided by Pierre Gillet with permission, © 2022. Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited. This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author.