Integrating Absolute Value Functions
Calculating ∫ abs(f(x)) dx
The function abs(f(x)) can be broken into two parts, depending on the sign of f(x):
abs(f(x)) =
{ f(x) when f(x) > 0
{ -f(x) when f(x) < 0
General procedure:
1. Find the roots of f(x).
2. Split the integral at the roots.
3. For areas where f(x)>0, calculate the sub-area ∫ f(x) dx.
4. For areas where f(x)<0, calculate the sub-area ∫ -f(x) dx.
5. Total all the sub-areas.
Let's illustrate this with examples. Screen shots are made with the HP Prime emulator. The absolute value function |f(x)| is graphed in blue, while f(x) is graphed in red (for illustrative purposes).
Example 1: ∫ |4x- 2| dx from x = 0 to x = 5
∫ |4x- 2| dx from x = 0 to x =5
The root of (4x - 2) is x = 1/2.
When x < 1/2, (4x - 2) < 0.
When x > 1/2, (4x - 2) > 0.
Break down the integral into:
∫ (|4x- 2| dx from x = 0 to x =5)
= ∫ ( -(4x- 2) dx from x = 0 to x =1/2) + ∫ (4x- 2 dx from x = 1/2 to x =5)
= 1/2 + 81/2
= 82/2
= 41
We can type in the entire integral into a calculator or app. Depending on the function and the advanced engine of the calculator, the accuracy may be affected. Calculators and apps with advanced engines include the HP Prime, Wolfram Alpha, and Desmos. (Your mileage may vary)
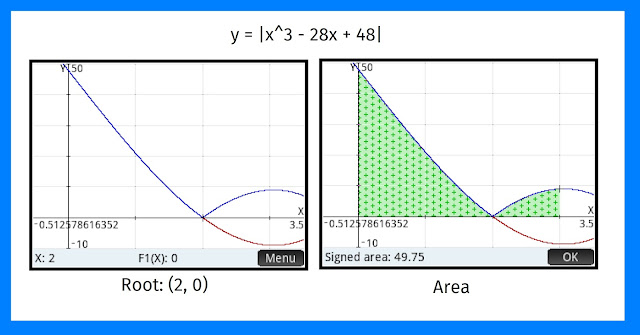
Example 2: ∫ |x^3 - 28x + 48| dx from x = 0 to x = 3
∫ |x^3 - 28x + 48| dx from x = 0 to x = 3
The roots of x^3 - 28x + 48 are at x = -6, x = 2, and x = 4. Since the root x = 2 is the only root in the interval [0, 3], this is the one root we are working with.
With root x = 2,
When x < 2, x^3 - 28x + 48 > 0
When x > 2, x^3 - 28x + 48 < 0
Then:
∫ ( |x^3 - 28x + 48| dx from x = 0 to x = 3 )
= ∫ ( (x^3 - 28x + 48) dx from x = 0 to x = 2 )
+ ∫ ( -(x^3 - 28x + 48) dx from x = 2 to x = 3 )
= 44 + 5.75
= 49.75
Example 3: ∫ |e^(2x) - 2| dx from x = 0 to x = 2
The root of e^(2x) - 2 is x = ln 2 ÷ 2 ≈ 0.34657
Let A = ln 2 ÷ 2, and with root x = A,
When x < A, e^(2x) - 2 < 0
When x > A, e^(2x) - 2 > 0
∫ ( |e^(2x) - 2| dx from x = 0 to x = 2 )
= ∫ ( -(e^(2x) - 2) dx from x = 0 to x = A ) + ∫( (e^(2x) - 2) dx from x = A to x = 2)
≈ 0.193147 + 22.99222
≈ 23.18537
Where is where this method returns approximates and using different calculators and apps may not produce the same results.
HP Prime: 23.1853693777
Desmos: 23.1853693777
Wolfram Alpha: 23.1853693776920
TI-30X Pro MathPrint: 23.18537052
Hope this technique helps,
Eddie
All original content copyright, © 2011-2023. Edward Shore. Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited. This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author.