A blog is that is all about mathematics and calculators, two of my passions in life.
Sunday, April 3, 2016
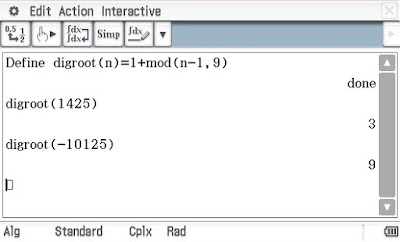
Casio Classpad fx-CP400: Defining Functions
Sunday, June 15, 2014
HP 15C: Area by Verticies With Curve Segments (with Jason Foose)
On June 6, 2014, I posted a revised program for the HP 15C to find the area of a polygon by given the coordinates of each vertex. You can see this post here:
http://edspi31415.blogspot.com/2014/06/hp-15c-area-of-polygon-by-vertices.html
Jason Foose, County Surveyor at Mohave County Public Works in Kingman, AZ contributed an addendum to the program: this allows you to enter curve segments and calculate the total area based on vertices and the curve segments. Jason Foose can be found on Google+ and on Linkedin.
General Instructions
The idea is to first enter all the coordinates of the vertices and calculate the area, then enter the curve segments and recalculate the area. Start at one at one point and work in either the clockwise or the counterclockwise motion.
Hence:
1. Enter initial coordinates (x0, y0): y0 ENTER x0 LBL A
2. Enter additional coordinates: y ENTER x LBL B
3. Calculate area with coordinates: LBL C
4. Enter radius and central angle, in HMS format: radius ENTER angle LBL D
5. Calculate final area: LBL E
When entering the radius and central angles, use positive values for radius for "outies", chord lines that add to the area. Use negative values for "innies", or chords that cut across the area. The 15C should be in Degrees mode.
The Expanded Program
Here is the program in full. Instructions in bold red are contributed by Jason Foose.
Memory registers used:
R0 = area
R1 = x_i
R2 = y_i
R3 = x_i+1
R4 = y_i+1
R5 = Σ (x_i * y_i+1) // ( i=1...n and cycle back to 1)
R6 = Σ (x_i+1 * y_i)
R7 = x_1
R8 = y_1
Program:
001 42, 21, 11 LBL A // enter initial vertex
002 0 0
003 44 5 STO 5
004 44 6 STO 6
005 33 R down // R↓
006 44 1 STO 1
007 44 7 STO 7
008 33 R down
009 44 2 STO 2
010 44 8 STO 8
011 43 32 RTN
012 42, 21, 12 LBL B // step 12 - add verticies
013 43 3 STO 3
014 45, 20, 2 RCL× 2
015 44, 40, 6 STO+ 6
016 33 R down
017 44 4 STO 4
018 45, 20, 1 RCL× 1
019 44, 40, 5 STO+ 5
020 45 4 RCL 4
021 44 2 STO 2
022 45 3 RCL 3
023 44 1 STO 1
024 43 32 RTN
025 42, 21, 13 LBL C // step 25 - calculate area with vertices
026 45 7 RCL 7
027 45, 20, 2 RCL× 2
028 44, 40, 6 STO+ 6
029 45 8 RCL 8
030 45, 20, 1 RCL× 1
031 44, 40, 5 STO+ 5
032 45, 5 RCL 5
033 45, 30, 6 RCL- 6
034 43 16 ABS
035 2 2
036 10 ÷
037 44 0 STO 0
Keystrokes:
Starting at Point (100, 100)
Coordinates:
100 ENTER 100 LBL A
100 ENTER 400 LBL B
200 ENTER 500 LBL B
300 ENTER 500 LBL B
300 ENTER 225 LBL B
425 ENTER 100 LBL B
LBL C \\ Area: 1.9011 acres
Add segments:
100 ENTER 90 LBL D \\ "outie" angle = 90
125 ENTER 90 CHS LBL D \\ "innie" angle = -90
LBL E \\ Area: 1.8643 acres
Special thanks to Jason Foose for the great addendum to the area by vertices program.
Eddie
Friday, June 6, 2014
HP 15C: Area of a Polygon by Vertices (revised)
HP 15C: Area of a Polygon by Vertices (revised)
In December 2011, I posted a program to calculate the area of a polygon given the vertices for the HP 15C. You can find the original program here:
http://edspi31415.blogspot.com/2011/12/hp-15c-programming-tutorial-part-15.html
The problem with this, that the area is not accurate when the initial point is not (0,0). This was brought up by Jason Foose. Jason, a million thanks.
Here is another attempt at it, this time it should work with any initial point. I tested the program with several different polygons and so far, so good.
Please test and let me know what you think. The instructions remain the same:
1. Enter the initial y coordinate, press ENTER, then enter the initial x coordinate, and press [ f ] [ √ ] (LBL A).
2. For each additional point, enter the y coordinate, press ENTER, then enter the x coordinate, and finally [ f ] [ e^x ] (LBL B).
3. To calculate the area, press [ f ] [10^x ] (LBL C).
Memory registers used:
R0 = area
R1 = x_i
R2 = y_i
R3 = x_i+1
R4 = y_i+1
R5 = Σ (x_i * y_i+1) // ( i=1...n and cycle back to 1)
R6 = Σ (x_i+1 * y_i)
R7 = x_1
R8 = y_1
Program - HP 15C:
LBL A
0
STO 5
STO 6
R down \\ R↓
STO 1
STO 7
R down
STO 2
STO 8
RTN
LBL B // step 12
STO 3
RCL× 2
STO+ 6
R down
STO 4
RCL× 1
STO+ 5
RCL 4
STO 2
RCL 3
STO 1
RTN
LBL C // step 25
RCL 7
RCL× 2
STO+ 6
RCL 8
RCL× 1
STO+ 5
RCL 5
RCL- 6
ABS
2
÷
STO 0
RTN
Total: 38 steps
Eddie
This blog is property of Edward Shore. 2014
Monday, July 30, 2012
Applications and Programming: Area of a Polygon Given the Coordinates of Vertices
Today's blog entry is how to find the area of an enclosed polygon, when you just know the vertices (corner points) of the polygon.
The area, with n vertices, is:
A ≈ 1/2 * | (x1 y0 - x0 y1) + (x2 y1 - x1 y2) + (x3 y2 - x2 y3) + ... + (x0 yn - xn y0) |
With | | representing the absolute value.
The sum ends with the last vertex of the set and the initial vertex. The calculation is a fairly simple one.
The following TI-84+ program handles this formula.
TI-84+ Program AREAVERT
: Input "X0:",X
: Input "Y0:",Y
: {X} → L1
: {Y} → L2
: 0 → T
: 1 → K
: Lbl Y
: 1+K→ K
: Input "NEXT X:", A
: Input "NEXT Y:", B
: augment(L1,{A})→ L1
: augment(L2,{B})→ L2
: T+A*L2(K-1)-B*L1(K-1)→ T
: Menu("MORE?","YES",Y,"NO",N)
: Lbl N
: T+X*L2(K)-Y*L1(K)→ T
: abs(T)/2→ T
: Disp "AREA=", T
: Pause
Notes:
* L1 is accessed by pressing [2nd], [ 1 ]
* L2 is accessed by pressing [2nd], [ 2 ]
* The program works best if you start with one vertex and cycle either clockwise or counterclockwise, and stay in one direction all the way through.
* The program will ask you if there are more vertices. You do not have to repeat the initial vertex in is program.
Example 1:
Find the area of a square with the vertices (0,0), (0,5), (5,5), and (5,0). This is a square with a side length of 5 units.
Area: 25.
Example 2:
Find the area of a polygon with vertices (-3,0), (3,0), (4,11), (2,15), and (-4,12).
Area: 95.5
Until next time,
Eddie
This blog is property of Edward Shore. © 2012
RPN HP 12C: Fibonacci and Lucas Sequences
RPN HP 12C: Fibonacci and Lucas Sequences Golden Ratio, Formulas, and Sequences Let φ be the Golden Ratio: φ = (1 + √5) ÷ 2...