HP Prime: Electric Field & Flux (Gauss’s Law)

HP Prime:  Electric Field & Flux (Gauss’s Law)

The program EFILED calculates the electric filed and flux for five common fields:

Ring

 Line or Wire of Charge  The radius of the Wire is small.

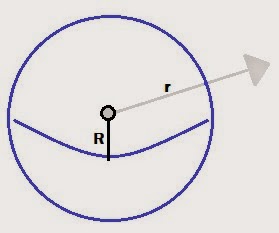
Sphere (non-conducting – uniform charge)

Plane (Flat Sheet)

Cylinder with the charge flowing through the ends

By Gauss’s Law, the general formula that of flux is:

Flux =  q/ε0 = ∫ E dA

Where:

q = charge (in Coulombs)

ε0 = 8.85418781762 * 10^-12 F/m

E = electric field

dA = change of area, where A represents Area

HP Prime: EFIELD

EXPORT EFIELD()

BEGIN

// Electric Filed & Flux

// EWS 2015-04-07

// SI Units ares assumed

// ε0=8.85418781762ᴇ−12_(F/m)

LOCAL c,ef,sa,flux;

// ef: electric field

// sa: surface area

// flux = ef * sa = q/ε

CHOOSE(c,"Elec. Field/Flux",

{"Ring","Line/Wire of Charge",

"Non-Conducting Sphere",

"Plane","Cylinder"});

IF c==0 THEN KILL; END;

// Ring

IF c==1 THEN

LOCAL ro,ri,a,q;

INPUT({ro,ri,a,q},"Elec. Filed: Ring",

{"ro=","ri=","a=","q="},

{"Outer Radius","Inner Radius",

"Point","Charge"});

ef:=q/(4*8.85418781762ᴇ−12*π*

((ro-ri)^2+a^2)^1.5);

sa:=π*(ro^2-ri^2);

END;

// Line/Wire of Charge

IF c==2 THEN

LOCAL l,r,a,y,q;

INPUT({l,r,a,q},"Elec. Field: Line",

{"l =","r =","a =","q ="},{"Length of Wire",

"Radius of Wire","Distance from Wire",

"Charge"});

ef:=(q*a)/(l*4*8.85418781762ᴇ−12*π)

*∫((y^2+a^2)^−1.5,y,−l/2,l/2);

sa:=π*l*2*π;

END;

// Non-Conducting Sphere

IF c==3 THEN

LOCAL R,r,q,p;

INPUT({R,r,q},"Non-Conducting Sphere",

{"R =","r =","q ="},{"Radius of Sphere",

"Radial Point","Charge"});

IF r<R THEN

sa:=4*π*r^2;

p:=q/(4/3*π*r^3);

ef:=(p*r)/(3*8.85418781762ᴇ−12);

ELSE

sa:=4*π*R^2;

p:=q/(4/3*π*R^3);

ef:=(p*R^3)/(3*8.85418781762ᴇ−12*r^2);

END;

END;

// Plane

IF c==4 THEN

LOCAL A,q;

INPUT({A,q},"Elec. Field: Plane",

{"A =","q ="},{"Sheet Area","Charge"});

ef:=q/(2*8.85418781762ᴇ−12*A);

sa:=A;

END;

// Cylinder

IF c==5 THEN

LOCAL R,r,L,q,p;

INPUT({R,r,L,q},"Non-Conducting Sphere",

{"R =","r =","L =","q ="},{

"Radius of Cylinder",

"Radial Point",

"Length of Cylinder",

"Charge"});

IF r<R THEN

sa:=2*π*r*L;

p:=q/(π*r^2*L);

ef:=(p*r)/(2*8.85418781762ᴇ−12);

ELSE

sa:=2*π*R*L;

p:=q/(π*R^2);

ef:=(p*R^2)/(2*8.85418781762ᴇ−12*r);

END;

END;

flux:=ef*sa;

PRINT();

PRINT("Electric Field: "+ef);

PRINT("Electric Flux: "+flux);

RETURN({ef, flux});

END;

Eddie

This blog is property of Edward Shore.  2015