TI-Nspire: Templates to Plot Functions, Parametric Equations, and Sequences
Introduction
The following are sample templates to plot functions in the form of y=f(x), parametric equations (x(t), y(t)), and one-level deep recurrence relations.
I used a while loop instead of a for loop because I tend to always use for loops, and working with integer objects can be quite difficult for non-Python experts like me.
The equations will be defined inside the script instead of having the user enter the script. . I am using the TI-NSpire CX II software 5.2.0771. I have programmed this with the TI-Nspire CX CAS software, but it should work on the non-CAS version.
As far as entering numbers at the input prompt, I have to enter approximations for π (which is approximately 3.1415926535).
The list.append(value) or list.append(list) adds the elements to the end of the list and the list is automatically saved.
The graphic commands uses a TI-specific module ti_plotlib. I have a lot of pleasure working with this module, with commands for clearing the graphic screen, automatically sizing the window, plotting the axes, with or without the numeric numeric endpoints, and set a color with RGB codes (any color you want).
You can download the file here: https://drive.google.com/file/d/1k_3lTVK5KK1ACXrVxemSWz_g-l8Nn62A/view?usp=sharing
The text of the scripts are presented below.
Plotting Functions - TI-Nspire CX II (CAS) Script: plotfxnspire.py
from math import *
import ti_plotlib as plt
# EWS 2020-12-28
# define function here
def f(x):
y=1/(x**2+1)
return y
# main routine
xa=float(input('start? '))
xb=float(input('stop? '))
n=float(input('n? '))
xc=(xb-xa)/n
# build
xp=xa
yp=f(xp)
xlist=[xp]
ylist=[yp]
while xp<xb:
xp=xp+xc
yp=f(xp)
xlist.append(xp)
ylist.append(yp)
# plot routine
# clear the screen
plt.cls()
# automatically fits the screen to fit the data
plt.auto_window(xlist,ylist)
# display the axes
# "on" plots axes and endpoints
# "axes" just plots the axes
plt.axes("on")
# select color - use RGB style
# denim blue
plt.color(21,96,189)
# plot the graph
plt.plot(xlist,ylist,".")
plt.show_plot()
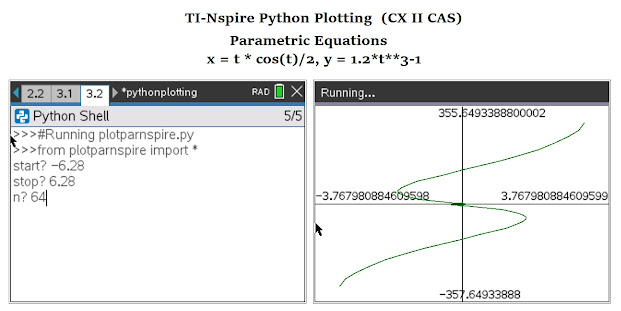
Plotting Parametric Equations - TI-Nspire CX II (CAS) Script: plotparnspire.py
from math import *
import ti_plotlib as plt
# EWS 2020-12-28
# define parametric here
def x(t):
x=t*cos(t)/2
return x
def y(t):
y=1.2*t**3-1
return y
# main routine
ta=float(input('start? '))
tb=float(input('stop? '))
n=float(input('n? '))
tc=(tb-ta)/n
# build
tp=ta
xp=x(tp)
yp=y(tp)
xlist=[xp]
ylist=[yp]
while tp<tb:
tp=tp+tc
xp=x(tp)
yp=y(tp)
xlist.append(xp)
ylist.append(yp)
# plot routine
# clear the screen
plt.cls()
# automatically fits the screen to fit the data
plt.auto_window(xlist,ylist)
# display the axes
# "on" plots axes and endpoints
# "axes" just plots the axes
plt.axes("on")
# select color - use RGB style
# mid green
plt.color(0,128,0)
# plot the graph
plt.plot(xlist,ylist,".")
plt.show_plot()
Plotting a Recurrence Relation- TI-Nspire CX II (CAS) Script: plotseqnspire.py
Use u for u_n-1. You should also be able to include n without problems.
from math import *
import ti_plotlib as plt
# EWS 2020-12-28
# define sequence here, u for u(n-1)
def w(u):
w=cos(u)+1
return w
# main routine
ui=float(input('initial? '))
n=float(input('n? '))
# build
xlist=[0]
ylist=[ui]
k=0
while k<n:
k=k+1
f=w(k)
xp=k
yp=f
xlist.append(xp)
ylist.append(yp)
# plot routine
# clear the screen
plt.cls()
# automatically fits the screen to fit the data
plt.auto_window(xlist,ylist)
# display the axes
# "on" plots axes and endpoints
# "axes" just plots the axes
plt.axes("on")
# select color - use RGB style
# orange
plt.color(255,127,39)
# plot the graph
plt.plot(xlist,ylist,".")
plt.show_plot()
Eddie
All original content copyright, © 2011-2021. Edward Shore. Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited. This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author.