Numworks: Rotated Plot - Python
Introduction
The script rotplot.py allows the user to choose between one of five equations and rotate the graph at a given angle. The equations are:
1. y = a + bx
2. y = ax^2 + bx + c
3. y = ax^3 + bx^2 + cx + d
4. y = a * sin(bx + c) + d
5. y = a * exp(bx + c ) + d
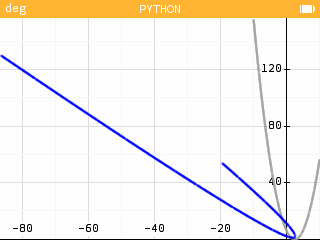
The original plot is in gray, the rotated plot is in blue.
Numworks Script: rotplot.py
(Size: 1,500 bytes)
from math import *
from matplotlib.pyplot import *
# 2021-04-18 EWS
print("Choose an equation.")
# define a,b,c,d
a=0
b=0
c=0
d=0
eq=6
while eq<1 or eq>5:
print("y=")
print("1. ax+b")
print("2. quadratic")
print("3. cubic")
print("4. a sin(bx+c)+d")
print("5. a exp(bx+c)+d")
eq=int(input())
a=float(input("a? "))
b=float(input("b? "))
if eq>=2:
c=float(input("c? "))
if eq>=3:
d=float(input("d? "))
p=float(input("Angle in degrees? "))
p=radians(p)
# main routine
xa=float(input('start? '))
xb=float(input('stop? '))
n=float(input('n? '))
xc=(xb-xa)/n
# define function here
def f(eq,a,b,c,d,x,p):
if eq==1:
y=a*x+b
if eq==2:
y=a*x**2+b*x+c
if eq==3:
y=a*x**3+b*x**2+c*x+d
if eq==4:
y=a*sin(b*x+c)+d
if eq==5:
y=a*exp(b*x+c)+d
xr=x*cos(p)-y*sin(p)
yr=x*sin(p)+y*cos(p)
return [x,y,xr,yr]
# build
flist=f(eq,a,b,c,d,xa,p)
xlist=[flist[0]]
ylist=[flist[1]]
xrlist=[flist[2]]
yrlist=[flist[3]]
xp=xa
# lists
while xp<xb:
xp=xp+xc
flist=f(eq,a,b,c,d,xp,p)
xlist.append(flist[0])
ylist.append(flist[1])
xrlist.append(flist[2])
yrlist.append(flist[3])
# plot routine
# set axes
x1x=min(xlist)
x1xr=min(xrlist)
x1=min(x1x,x1xr)
y1x=min(ylist)
y1xr=min(yrlist)
y1=min(y1x,y1xr)
x2x=max(xlist)
x2xr=max(xrlist)
x2=max(x2x,x2xr)
y2x=max(ylist)
y2xr=max(yrlist)
y2=max(y2x,y2xr)
axis((x1,x2,y1,y2))
axis(True)
grid(True)
# plot points
plot(xlist,ylist,color='gray')
plot(xrlist,yrlist,color='blue')
show()
Download the script here: https://workshop.numworks.com/python/ews31415/rotplot
Eddie
All original content copyright, © 2011-2021. Edward Shore. Unauthorized use and/or unauthorized distribution for commercial purposes without express and written permission from the author is strictly prohibited. This blog entry may be distributed for noncommercial purposes, provided that full credit is given to the author.